如图,在平面直角坐标系xOy中,抛物线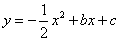 与x轴交于A(1,0)、B(5,0)两点.
与x轴交于A(1,0)、B(5,0)两点.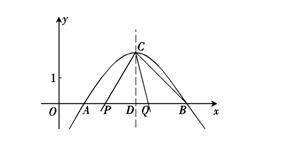
(1). 求抛物线的解析式和顶点C的坐标;
(2). 设抛物线的对称轴与x轴交于点D,将∠DCB绕点C按顺时针方向旋转,角的两边CD和CB与x轴分别交于点P、Q,设旋转角为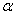 (0°<
(0°<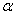 <90°)
<90°)
①当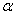 等于多少度时,△CPQ是等腰三角形?
等于多少度时,△CPQ是等腰三角形?
②设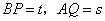 ,求s与t之间的函数关系式.
,求s与t之间的函数关系式.
相关知识点
推荐套卷
如图,在平面直角坐标系xOy中,抛物线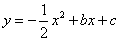 与x轴交于A(1,0)、B(5,0)两点.
与x轴交于A(1,0)、B(5,0)两点.
(1). 求抛物线的解析式和顶点C的坐标;
(2). 设抛物线的对称轴与x轴交于点D,将∠DCB绕点C按顺时针方向旋转,角的两边CD和CB与x轴分别交于点P、Q,设旋转角为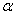 (0°<
(0°<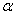 <90°)
<90°)
①当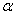 等于多少度时,△CPQ是等腰三角形?
等于多少度时,△CPQ是等腰三角形?
②设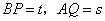 ,求s与t之间的函数关系式.
,求s与t之间的函数关系式.