初中数学圆幂定理填空题

如图，AB是⊙O的直径，且经过弦CD的中点H，过CD延长线上一点E作⊙O的切线，切点为F．若∠ACF=65°，则∠E=         ．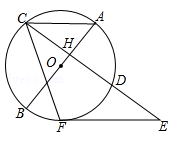

如图，在圆心角为的扇形OAB中，半径OA=2，C为弧AB的中点，D，E分别是OA，OB的中点，则图中阴影部分的面积为        ．

如图，边长为1的菱形ABCD的两个顶点B、C恰好落在扇形AEF的弧EF上．若∠BAD=120°，则弧BC的长度等于    （结果保留π）．

如图是一个古代车轮的碎片，小明为求其外圆半径，连接外圆上的两点A、B，并使AB与车轮内圆相切于点D，半径为OC⊥AB交外圆于点C．测得CD=10cm，AB=60cm，则这个车轮的外圆半径是           ．

如图，点O为所在圆的圆心，∠BOC=112°，点D在BA的延长线上，AD=AC，则∠D=         ．

如图，三个小正方形的边长都为1，则图中阴影部分面积的和是    （结果保留π）．

如图，⊙O是△ABC的外接圆，AD是⊙O的直径，若⊙O的半径是4，sinB=，则线段AC的长为     ．

用一个圆心角为90°，半径为4的扇形围成一个圆锥的侧面，该圆锥底面圆的半径     ．

如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，连接AC．若∠CAB=22.5°，CD=8cm，则⊙O的半径为       cm．

如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，若∠C=20°，则∠CDA=         °．

如图，已知AB是⊙O的直径，点C在⊙O上，若∠CAB=40°，则∠ABC的度数为     ．

已知圆锥的底面半径是1cm，母线长为3cm，则该圆锥的侧面积为     cm²．

如图，AB是⊙O的直径，弦CD⊥AB于点E，若AB=8，CD=6，则BE=     ．

如图，AD是⊙O的直径，弦BC⊥AD于E，AB=BC=12，则OC=      ．

如图，PA是⊙O的切线，切点为A，PO的延长线交⊙O于点B．若∠ABP=33°，则∠P=       °．