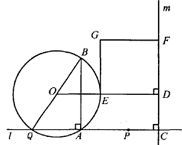
(本题14分)如图,点A和动点P在直线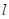 上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O。点C在点P右侧,PC=4,过点C作直线
上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O。点C在点P右侧,PC=4,过点C作直线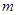 ⊥
⊥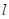 ,过点O作OD⊥
,过点O作OD⊥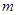 于点D,交AB右侧的圆弧于点E。在射线CD上取点F,使DF=
于点D,交AB右侧的圆弧于点E。在射线CD上取点F,使DF=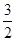 CD,以DE,DF为邻边作矩形DEGF,设AQ=
CD,以DE,DF为邻边作矩形DEGF,设AQ=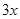
(1)用关于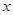 的代数式表示BQ,DF;
的代数式表示BQ,DF;
(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长;
(3)在点P的整个运动过程中,
①当AP为何值时,矩形DEGF是正方形?
②作直线BG交⊙O于另一点N,若BN的弦心距为1,求AP的长(直接写出答案)
(本小题满分9分)如图11,在△ABC中,BC是以AB为直径的⊙O的切线,且⊙O与AC相交于点D,E为BC的中点,连接DE.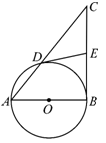
(1)求证:DE是⊙O的切线;
(2)连接AE,若∠C=45°,求sin∠CAE的值.
如图,⊙M与x轴交于A、B两点,其坐标分别为 、
、 ,直径CD⊥x轴于N,抛物线
,直径CD⊥x轴于N,抛物线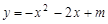 经过A、B、D三点,
经过A、B、D三点,
(1)求m的值及点D的坐标.
(2)若直线CE切⊙M于点C,G在直线CE上,已知点G的横坐标为3.求G的纵坐标
(3)对于(2)中的G,是否存在过点G的直线,使它与(1)中抛物线只有一个交点,请说明理由.
(4)对于(2)中的G直线FG切⊙M于点F,求直线DF的解析式.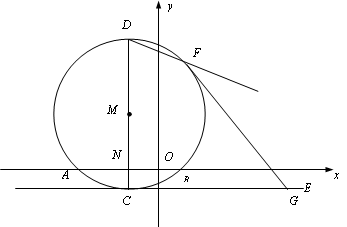
如图,在平面直角坐标系中,⊙O的圆心在坐标原点,半径为3.过A(-7,9),B(0,9)的抛物线 (a,b,c为常数,且a≠0)与x轴交于D,E (点D在点E右边)两点,连结AD.
(a,b,c为常数,且a≠0)与x轴交于D,E (点D在点E右边)两点,连结AD.
(1)若点D的坐标为D(3,0).①请直接写出此时直线AD与⊙O的位置关系;②求此时抛物线对应的函数关系式;
(2)若直线AD和⊙O相切,求抛物线二次项系数a的值;
(3)当直线AD和⊙O相交时,直接写出a的取值范围.
如图,海边有两个灯塔A,B.即将靠岸的轮船得到信息:海里有一个以AB为弦的弓形暗礁区域,要求轮船在行驶过程中,对两灯塔的张角不能超过 .当轮船航行到P点时,测得轮船对两灯塔的张角∠APB刚好等于
.当轮船航行到P点时,测得轮船对两灯塔的张角∠APB刚好等于 .
.
(1)请用直尺和圆规在图中作出△APB的外接圆 (作出图形,不写作法,保留痕迹);
(2)若此时轮船到B的距离PB为700米,已知AB=500米,求出此时轮船到A的距离.
如图1,已知在平行四边形ABCD中,AB=10,BC=16,sinB= ,点P是边BC上的动点,以CP为半径的圆C与边AD交于点E、F(点F在点E的右侧),射线CE与射线BA交于点G.
,点P是边BC上的动点,以CP为半径的圆C与边AD交于点E、F(点F在点E的右侧),射线CE与射线BA交于点G.

(1)当圆C经过点A时,求CP的长;
(2)联结AP,当AP∥CG时,求弦EF的长;
(3)当△AGE是等腰三角形时,求CG的长.
如图,已知等边△ABC,AB=16,以AB为直径的半圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连结GD.
(1)求证:DF是⊙O的切线;
(2)求FG的长;
(3)求tan∠FGD的值.
在直角坐标系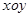 中,已知点P是反比例函数
中,已知点P是反比例函数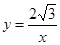 (
(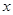 >0)图象上一个动点,以P为圆心的圆始终与
>0)图象上一个动点,以P为圆心的圆始终与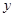 轴相切,设切点为A.
轴相切,设切点为A.
(1)如图1,⊙P运动到与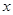 轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由.
轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由.
(2)如图2,⊙P运动到与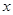 轴相交,设交点为B,C.当四边形ABCP是菱形时:
轴相交,设交点为B,C.当四边形ABCP是菱形时:
①求出点A,B,C的坐标.
②在过A,B,C三点的抛物线上是否存在点M,使△MBP的面积是菱形ABCP面积的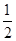 .若存在,试求出所有满足条件的M点的坐标,若不存在,试说明理由.
.若存在,试求出所有满足条件的M点的坐标,若不存在,试说明理由.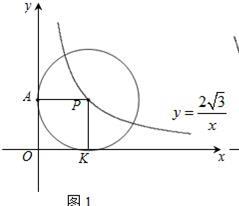
如图,C为以AB为直径的⊙O上一点,AD和过点C的切线互相垂直,垂足为点D.
(1)求证:AC平分∠BAD;
(2)若CD=3,AC= ,求⊙O 的半径长.
,求⊙O 的半径长.
(本题10分)如图,已知等边ΔABC,以AB为直径的半圆与BC边交于点D,过点D作⊙O的切线 DF交AC于点F,过点D作DE⊥AB, 垂足为点E,过点F作FG⊥AB,垂足为点G,连结GD.
(1)求证:DF⊥AC;
(2)若AB=8,求tan∠FGD的值.
如图,AB是⊙O的直径,BC交⊙O于点D,E是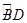 的中点,连接AE交BC于点F,∠ACB=2∠EAB.
的中点,连接AE交BC于点F,∠ACB=2∠EAB. 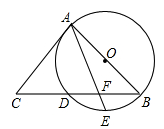
(1)求证:AC是⊙O的切线;
(2)若cosC=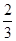 ,AC=6,求BF的长.
,AC=6,求BF的长.
如图所示,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
(1)求证:BC是⊙O的切线;
(2)连接AF,BF,求∠ABF的度数;
(3)如果CD=15,BE=10,sinA= ,求⊙O的半径
,求⊙O的半径
半径为2cm的⊙O与边长为2cm的正方形ABCD在水平直线 的同侧,⊙O与
的同侧,⊙O与 相切于点F,DC在
相切于点F,DC在 上,若BE切⊙O于点E.
上,若BE切⊙O于点E.
(Ⅰ)如图1,当点A在⊙O上时,∠EBA=________度;
(Ⅱ)如图2,当E,A,D三点在同一直线上时,求线段OA的长.
如图,AB是⊙O的直径,C、D在⊙O上,连结BC,过D作PF∥AC交AB于E,交⊙O于F,交BC于点G,交过B点的直线于点P,且∠BPF=∠ADC.
(1)判断直线BP与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为 ,AC=2,BE=1,求BP的长.
,AC=2,BE=1,求BP的长.
如图, ,C、D是
,C、D是 的三等分点,AB分别交OC、OD于点E、F,求证:AE=CD.
的三等分点,AB分别交OC、OD于点E、F,求证:AE=CD.