初中数学圆幂定理试题

如图，已知AB为⊙O的直径，E是AB延长线上一点，点C是⊙O上的一点，连结EC、BC、AC，且∠BCE＝∠BAC.
（1）求证：EC是⊙O的切线.
（2）过点A作AD垂直于直线EC于D，若AD＝3，DE＝4，求⊙O的半径.

如图，在平面直角坐标系中，O为坐标原点，点A、B的坐标分别为（8，0）、（0，6）．动点Q从点O、动点P从点A同时出发，分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动，运动时间为t（秒）（0＜t≤5）．以P为圆心，PA长为半径的⊙P与AB、OA的另一个交点分别为C、D，连接CD、QC．
（1）求当t为何值时，点Q与点D重合？
（2）设△QCD的面积为S，试求S与t之间的函数关系式，并求S的最大值；
（3）若⊙P与线段QC只有一个交点，请直接写出t的取值范围．

如图，在Rt△ABC中，∠C=90°，∠A=30°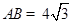，．若动点D在线段AC上（不与点A、C重合），过点D作DE⊥AC交AB边于点E．
（1）当点D运动到线段AC中点时，DE=　　；
（2）点A关于点D的对称点为点F，以FC为半径作⊙C，当DE=　　时，⊙C与直线AB相切．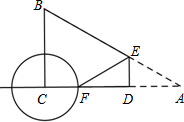

如图，已知⊙O的直径AB=6，E、F为AB的三等分点，M、N为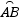上两点，且∠MEB=∠NFB=60°，则EM+FN=　　．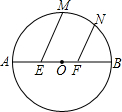

如图（a），有一张矩形纸片ABCD，其中AD=6cm，以AD为直径的半圆，正好与对边BC相切，将矩形纸片ABCD沿DE折叠，使点A落在BC上，如图（b）．则半圆还露在外面的部分（阴影部分）的面积为　     　．

如图，△ABC是⊙O内接正三角形，将△ABC绕点O顺时针旋转30°得到△DEF，DE分别交AB，AC于点M，N，DF交AC于点Q，则有以下结论：①∠DQN=30°；②△DNQ≌△ANM；③△DNQ的周长等于AC的长；④NQ=QC．其中正确的结论是　   　．（把所有正确的结论的序号都填上）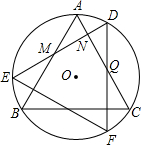

如图，四边形ABCD是菱形，∠A=60°，AB=2，扇形BEF的半径为2，圆心角为60°，则图中阴影部分的面积是（　　）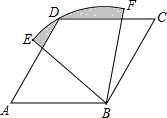

A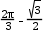．	B．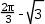
C．	D．

如图，点在轴的正半轴上，，，.点从点出发，沿轴向左以每秒1个单位长的速度运动，运动时间为秒.

（1）求点的坐标；
（2）当时，求的值；
（3）以点为圆心，为半径的随点的运动而变化，当与四边形的边（或边所在的直线）相切时，求的值．

如图，在中，AB=AC，以AB为直径的交BC于点M，于点N.

(1)求证：MN是⊙O的切线；
(2)若，AB=2，求图中阴影部分的面积.

如图，在△ABC中，AB=AC，∠BAC=54°，以AB为直径的 ⊙O分别交AC，BC于点D，E，过点B作⊙O的切线，交AC的延长线于点F．

⑴求证：BE=CE；
⑵求∠CBF的度数；
⑶若AB=6，求的长.

如图⊙O是∆ABC的外接圆，且AB=AC，点D在弧BC上运动，过点D作DE//BC，DE交AB的延长线于点E，连结AD、BD

（1）求证∠ADB=∠E；
（2）当点D运动到什么位置时，DE是⊙O的切线？请说明理由；
（3）当AB=5，BC=6时，求⊙O的半径.

为了测量一个圆形铁环的半径，某同学采用如下的方法：将铁环放在水平桌面上，用一个锐角为30⁰的三角板和一把刻度尺，按如图所示的方法得到相关数据，若三角形、刻度尺均与圆相切（切点为B、P），且测得PA=5，则铁环的半径为_________（保留根号）.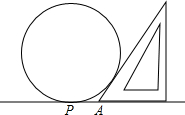

如图，在△ABC中，BE是它的角平分线，∠C＝90°，D在AB边上，以DB为直径的半圆O经过点E，交BC于点F.

(1)求证：AC是⊙O的切线；
(2)已知sin A＝，⊙O的半径为4，求图中阴影部分的面积．

如图，在半径为5的⊙O中，AB、CD是互相垂直的两条弦，垂足为P，且AB＝CD＝8，则OP的长为  (　　)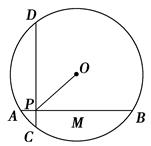

A．3         B．4
C．3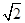    D．4

如图，在梯形ABCD中，AB∥CD，AD＝BC，将△ACD沿对角线翻折后，点D恰好与边AB的中点M重合．

(1)点C是否在以AB为直径的圆上？请说明理由．
(2)当AB＝4时，求此梯形的面积．