如图,直线 与
与 轴、
轴、 轴分别相交于
轴分别相交于 两点,圆心
两点,圆心 的坐标为
的坐标为 ,圆
,圆 与
与 轴相切于点
轴相切于点 .若将圆
.若将圆 沿
沿 轴向左移动,当圆
轴向左移动,当圆 与该直线相交时,横坐标为整数的点
与该直线相交时,横坐标为整数的点 的个数是( )
的个数是( )
| A.2 | B.3 | C.4 | D.5 |
如图,以线段 为直径的⊙
为直径的⊙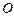 交线段
交线段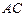 于点
于点 ,点
,点 是弧AE的中点,
是弧AE的中点,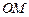 交
交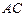 于点
于点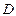 ,
,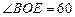 °,
°, ,
,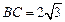 .
.
(1)求 的度数;
的度数;
(2)求证:BC是⊙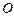 的切线;
的切线;
(3)求MD的长度.
将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为()
A.15 B.28
B.28 C.29
C.29 D.34
D.34
有下列四个命题:①直径是弦;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.其中正确的有
| A.4个 | B.3个 | C.2个 | D.1个 |
如图10-1,在平面直角坐标系 中,点
中,点 在
在 轴的正半轴上, ⊙
轴的正半轴上, ⊙ 交
交 轴于
轴于  两点,交
两点,交 轴于
轴于 两点,且
两点,且 为
为 的中点,
的中点, 交
交 轴于
轴于 点,若点
点,若点 的坐标为(-2,0),
的坐标为(-2,0),


(1)(3分)求点 的坐标.
的坐标.
(2)(3分)连结 ,求证:
,求证: ∥
∥
(3)(4分) 如图10-2,过点 作⊙
作⊙ 的切线,交
的切线,交 轴于点
轴于点 .动点
.动点 在⊙
在⊙ 的圆周上运动时,
的圆周上运动时, 的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
如图,在平面直角坐标系中,坐标原点为 ,
, 点坐标为
点坐标为 ,
, 点坐标为
点坐标为 ,以
,以 的中点
的中点 为圆心,
为圆心, 为直径作⊙P与
为直径作⊙P与 轴的正半轴交于点
轴的正半轴交于点 .
.
(1)求经过 三点的抛物线对应的函数表达式.
三点的抛物线对应的函数表达式.
(2)设 为(1)中抛物线的顶点,求直线
为(1)中抛物线的顶点,求直线 对应的函数表达式.
对应的函数表达式.
(3)试说明直线 与⊙P的位置关系,并证明你的结论.
与⊙P的位置关系,并证明你的结论.