初中数学三角形的五心试题

如图，一根木棒AB的长为2m斜靠在与地面垂直的墙上，与地面的倾斜角∠ABO为60°，当木棒沿墙壁向下滑动至A′，AA′=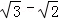，B端沿地面向右滑动至点B′，则木棒中点从P随之运动至P′所经过的路径长为（ ）

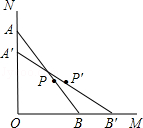
A．1

B．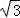

C．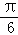

D．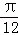

已知正n边形的每一个内角都等于144°，则n为（ ）

A．9

B．10

C．12

D．15

如图，在平面直角坐标系中，直线AB与x轴，y轴分别交于点A（4，0），B（0，3）．点C的坐标为（0，m），过点C作CE⊥AB于点E，点D为x轴正半轴的一动点，且满足OD=2OC，连结DE，以DE，DA为边作▱DEFA．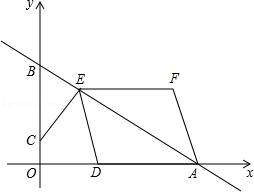

（1）当m=1时，求AE的长．
（2）当0＜m＜3时，若▱DEFA为矩形，求m的值；
（3）是否存在m的值，使得▱DEFA为菱形？若存在，直接写出m的值；若不存在，请说明理由．

如图，点A是5×5网格图形中的一个格点，图中每个小正方形的边长为1，请在网格中按下列要求操作：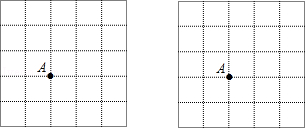

（1）以点A为其中的一个顶点，在图（1）中画一个面积等于3的格点直角三角形；
（2）以点A为其中的一个顶点，在图（2）中画一个面积等于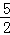的格点等腰直角三角形．

已知D、E分别是△ABC的AB、AC中点，则S_△ADE：S_{四边形DBCE}=           ．

如图，在△ABC中，AD⊥CA于点A，交BC于点D，M是CD的中点，连接AM，AM=AB．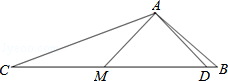

（1）求证：CD=2AB；
（2）若AC=8，AB=5，求AD的长．

已知：如图，△AOC≌△BOD．求证：△AOD≌△BOC．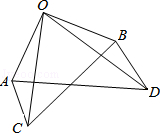

如图，在Rt△ABC中，∠C=90°，AB=10cm，D为AB的中点，则CD=      cm．

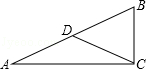
如图，在△ABC中，AB＝AC，点D、E、F分别在AB、BC、AC上，且BE＝CF，AD＋EC＝AB．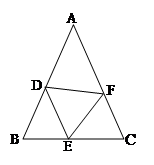

（1）求证：△DEF是等腰三角形；
（2）当∠A＝40°时，求 ∠DEF的度数；
（3）△DEF可能是等腰直角三角形吗？为什么？

如图，在△ABC中，AD是BC上的高，AE平分∠BAC，∠B＝75°， ∠C＝45°．求∠DAE与∠AEC的度数．

如图，在△ADC中，AD＝BD＝BC，∠C＝30°，则∠ADB＝_____．

如图，在△ABC中，∠A＝30°，∠B＝50°，延长BC到D，则∠ACD＝_____．

如图，AB∥EF∥DC，∠ABC＝90°，AB＝DC，那么，图中的全等三角形共有（    ）

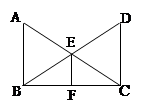
A．1 对	B．2对
C．3对	D．4对

已知△ABC中，2（∠B＋∠C）＝3∠A，则∠A 的度数是（   ）
A．54°          B．72°        C．108°       D．144°

若等腰三角形的一个底角的度数为72°，则顶角的度数为（   ）

A．108°

B．72°

C．54°

D．36°