初中数学三角形的五心解答题

如图，在△ABC中，AB=AC=13厘米，BC=10厘米，AD⊥BC于点D，动点P从点A出发以每秒1厘米的速度在线段AD上向终点D运动。设动点运动时间为t秒。
（1）求AD的长．
（2）当△PDC的面积为15平方厘米时，求的值．
（3）动点M从点C出发以每秒2厘米的速度在线段CB上运动．点M与点P同时出发，且当点P运动到终点D时，点M也停止运动。是否存在t，使得S_△PMD＝S_△ABC？若存在，请求出t的值；若不存在，请说明理由．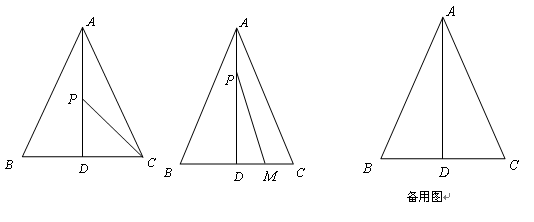

我们知道当人的视线与物体表面互相垂直时的视觉效果最佳．如图是小明站在距离墙壁1.60米处观察装饰画时的示意图，此时小明的眼睛与装饰画底部A处于同一水平线上，视线恰好落在装饰画中心位置E处，且与AD垂直.已知装饰画的高度AD为0.66米，
求：⑴ 装饰画与墙壁的夹角∠CAD的度数（精确到1°）；
⑵ 装饰画顶部到墙壁的距离DC（精确到0.01米）.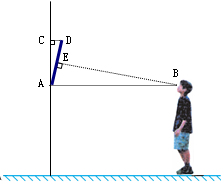
 

两条并行线上共有k个点，用这k个点恰可以连接1309个三角形，那么k是多少？

如图，设ABCD是正方形，P是CD边的中点，点Q在BC边上，
且ÐAPQ=90°，AQ与BP相交于点T，则的值为多少？

已知四边形ABCD中AD//BC，AD：BC=1：2，S_DAOF：S_DDOE=1：3，S_DBEF="24" cm²，求rAOF的面积。

两条并行线上共有k个点，用这k个点恰可以连接1309个三角形，那么k是多少？

(25分)已知G是△ABC内任一点，BG、CG分别交AC、AB于点E、F.
求使不等式S_△BGF·S_△CGE≤kS²_△ABC恒成立的k的最小值.

已知△ABC中，∠A>∠B>∠C，且∠A=2∠B.若三角形的三边长为整数，面积也为整数，求△ABC面积的最小值.