初中数学三角形的五心解答题

已知：如图，AB＝AC,AE＝AD，点D、E分别在AB、AC上．求证：∠B＝∠C．

如图，AB∥CD，AB=CD，点E、F在AD上，且AE=DF．
求证：△ABE≌△DCF．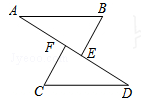

已知：如图，点A，D，C在同一直线上，AB∥EC，AC=CE，∠B=∠EDC
求证：BC=DE

已知：如图，AB∥DE，AB=DE，AF=DC．求证：≌．

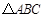如图，与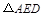均是等边三角形，连接BE、CD．请在图中找出一条与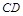长度相等的线段，并证明你的结论．
结论：
证明：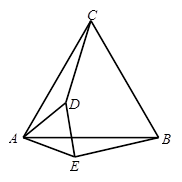

如图，已知△ABC，请用尺规过点A作一条直线，使其将△ABC分成面积相等的两部分，（保留作图痕迹，不写作法）

如图，四边形ABCD是菱形，CE⊥AB交AB延长线于E，CF⊥AD交AD延长线于F，
求证：CE=CF。

如图1，在△ABC中，AB=AC，点D，E分别在AB和AC上，且∠ADC=∠AEB=90°，则CD=BE．探究发现：如图2，在△ABC中，仍然有条件“AB=AC，点D，E分别在AB和AC上”．若∠ADC＋∠AEB=180°，则CD与BE是否仍相等？若相等，请证明；若不相等，请举反例说明．

有一块直角三角形的绿地，量得两直角边长分别为3m，4m现在要将绿地扩充成等腰三角形，且扩充部分是以4m为直角边的直角三角形，求扩充后等腰三角形绿地的周长．

如图，点A、F、C、D在同一直线上，点B和点E分别在直线AD的两侧，且AB=DE，∠A=∠D，AF=DC．
求证：△ABC≌△DEF;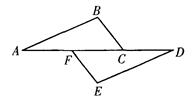

如图，已知∠B=∠C，AD=AE，则AB=AC，请说明理由（填空）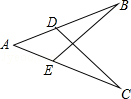

解：在△ABC和△ACD中，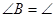
    （     ）
    （     ）
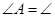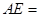       （已知）
∴△ABE≌△ACD （     ）
∴AB=AC（                      ）

如图，C为线段AB的中点，CD平分∠ACE，CE平分∠BCD，且CD＝CE，求证：△ACD≌△BCE．

如图，在ΔABC与ΔDCB 中，AC与BD 交于点E，且，∠A=∠D，AB=DC．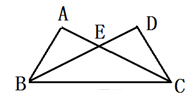

（1）求证：ΔABE≌ΔDCE
（2）当∠AEB=70°时，求∠EBC的度数．

如图，已知:EC=AC，∠BCE=∠DCA，∠A=∠E。求证：∠B=∠D．

已知CE=CB，∠1=∠2，AC= DC，  求证：AB=DE.