已知四条直线y=kx+3,y=1,y=-3和x=-1所围成的四边形的面积是8,则k的值为
甲、乙两人骑车从学校出发,先上坡到距学校6千米的A地,再下坡到距学校16千米的B地,甲、乙两人行程y (千米)与时间x (小时)之间的函数关系如图所示.若甲、乙两人同时从 地按原路返回到学校,返回时,甲和乙上、下坡的速度仍保持不变.则下列结论:①乙往返行程中的平均速度相同;②乙从学校出发45分钟后追上甲;③乙从
地按原路返回到学校,返回时,甲和乙上、下坡的速度仍保持不变.则下列结论:①乙往返行程中的平均速度相同;②乙从学校出发45分钟后追上甲;③乙从 地返回到学校用时1小时18分钟;④甲、乙返回时在下坡路段相遇.其中正确的结论有 ▲ (填“序号”)
地返回到学校用时1小时18分钟;④甲、乙返回时在下坡路段相遇.其中正确的结论有 ▲ (填“序号”)
直线y=mx+n和直线y=kx在同一坐标系中的图象如图10所示,则关于x的不等式mx+n>kx的解集是 。
若一次函数y=ax+1-a中,y随x的增大而增大,且它的图象与y轴交于正半轴,则实数a的取值范围是 。
函数y=k(x-1)的图象向左平移一个单位后与反比例函数y= 的图象的交点为A、B,若点A的坐标为(1,2),则点B的坐标为_______.
的图象的交点为A、B,若点A的坐标为(1,2),则点B的坐标为_______.
在一次运输任务中,一辆汽车将一批货物从A地运往B地,到达B地卸货后返回.设汽车从A地出发 时,汽车与A地的距离为
时,汽车与A地的距离为 ,
, 与
与 的函数关系如图所示.
的函数关系如图所示.
请你分别求出这辆汽车往、返的速度;
直接写出
 与
与 的函数关系式;
的函数关系式;求这辆汽车从A地出发6小时与A地的距离.
在平面直角坐标系 中,正方形
中,正方形 、
、 、
、 ,…,按右图所示的方式放置.点
,…,按右图所示的方式放置.点 、
、 、
、 ,…和点
,…和点 、
、 、
、 ,…分别在直线
,…分别在直线 和
和 轴上.已知
轴上.已知 (1,
(1, ),
), (
( ,
, ),则点
),则点 的坐标是______________;点
的坐标是______________;点 的坐标是___________.
的坐标是___________.
如图,直线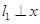 轴于点
轴于点 ,直线
,直线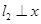 轴于点
轴于点 ,直线
,直线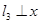 轴于点
轴于点 ,…直线
,…直线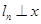 轴于点
轴于点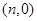 .函数
.函数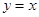 的图象与直线
的图象与直线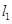 ,
, ,
,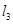 ,…
,… 分别交于点
分别交于点 ,
,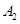 ,
,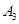 ,…
,…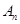 ;函数
;函数 的图象与直线
的图象与直线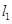 ,
, ,
,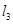 ,…
,… 分别交于点
分别交于点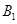 ,
,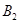 ,
, ,…
,…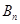 .如果
.如果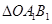 的面积记作
的面积记作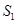 ,四边形
,四边形 的面积记作
的面积记作 ,四边形
,四边形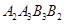 的面积记作
的面积记作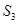 ,…四边形
,…四边形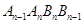 的面积记作
的面积记作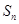 ,那么S2012= .
,那么S2012= . 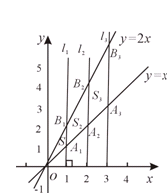
如图,已知直线 交x轴、y轴于点A、B,⊙P的半径为1,圆心从原点出发以每秒1个单位的速度向x轴正方向移动,移动时间为t(s),则t = s时⊙P与直线AB只有一个公共点.
交x轴、y轴于点A、B,⊙P的半径为1,圆心从原点出发以每秒1个单位的速度向x轴正方向移动,移动时间为t(s),则t = s时⊙P与直线AB只有一个公共点.
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,……,按如图所示的方式放置.点A1,A2,A3,……,和点C1,C2,C3,……,分别在直线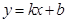 (k>0)和x轴上,已知正方形
(k>0)和x轴上,已知正方形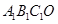 和正方形A2B2C2C1的面积分别是4和16,则Bn的坐标是
和正方形A2B2C2C1的面积分别是4和16,则Bn的坐标是 
如图,在平面直角坐标系中,O为坐标原点,B(5,0),M为等腰梯形OBCD底边OB上一点,OD=BC=2,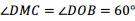 .
.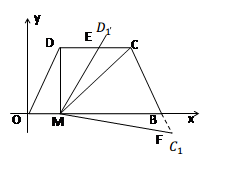
(1)求直线CB的解析式;
(2)求点M的坐标
(3)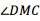 绕点M顺时针旋转
绕点M顺时针旋转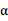 (30
(30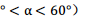 到
到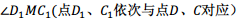 ,射线
,射线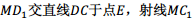 交直线CB于点F,设DE=m,BF=n,求m与n的函数关系式.
交直线CB于点F,设DE=m,BF=n,求m与n的函数关系式.