[江苏]2012年江苏省南京市溧水县中考二模数学试卷
要了解全校学生的课外作业负担情况,你认为以下抽样方法中比较合理的是( )
| A.调查全体女生 | B.调查全体男生 |
| C.调查九年级全体学生 | D.调查七、八、九年级各50名学生 |
据扬子晚报报道,2012年5月7日南京市最高气温是33℃,最低气温是22℃,则当天南京市气温 (℃)的变化范围可用不等式表示为( )
(℃)的变化范围可用不等式表示为( )
| A.t≥22 | B.t≤22 | C.22<t<33 | D.22≤t≤33 |
如图,△ABC是⊙O的内接三角形,将△ABC绕圆心O逆时针方向旋转α°(0<α<90),得到△A′B′C′,若⌒AB′=⌒A′C=⌒C′B,则∠B的度数为( )
| A.30° | B.45° | C.50° | D.60° |

正方形A1B1C1O,A2B2C2C1,A3B3C3C2,……,按如图所示的方式放置.点A1,A2,A3,……,和点C1,C2,C3,……,分别在直线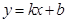 (k>0)和x轴上,已知正方形
(k>0)和x轴上,已知正方形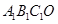 和正方形A2B2C2C1的面积分别是4和16,则Bn的坐标是
和正方形A2B2C2C1的面积分别是4和16,则Bn的坐标是 
2012年南京市初中毕业生升学体育考试要求男生从立定跳远、投掷实心球等6个项目中任选三项.某校九年级共有100名男生选择了立定跳远,现从这100名男生中随机抽取10名男生进行测试,下面是他们测试结果的条形统计图.(另附:九年级男生立定跳远的计分标准)
九年级男生立定跳远计分标准
| 成绩(cm) |
230 |
190 |
172 |
164 |
… |
| 分值 |
13 |
12 |
11 |
10 |
… |
求这10名男生在本次测试中,立定跳远距离的极差和中位数,立定跳远得分的众数和平均数.
请你估计该校选择立定跳远的100名男生中立定跳远得12分的人数.
如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE.已知∠BAC=30º,EF⊥AB,垂足为F,连结DF.

求证:AC=EF;
求证:四边形ADFE是平行四边形.
小明与小红共同发明了一种“字母棋”,进行比胜负的游戏.他们用三种字母做成5只棋子(棋子除字母外其它均相同),其中A棋1只,B棋2只,C棋2只.
“字母棋”的游戏规则为:
随机从5只棋子中摸出两只棋子,若摸到A棋,则小明胜;若摸到两只相同的棋子,则小红胜.其余情况则为平局.
你认为这个游戏公平吗?请说明理由,若不公平请修改游戏规则使游戏公平.
在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.
根据图像信息,解答下列问题:这辆汽车的往、返速度是否相同?请说明理由;
求返程中y与x之间的函数表达式;
求这辆汽车从甲地出发4h时与甲地的距离.

如图,用总长度为12米的不锈钢材料设计成外观为矩形的框架.当竖档AB为多少时,矩形框架ABCD的面积为3平方米?(题中的不锈钢材料总长度指图中所有黑线的长度和,所有横档和竖档分别与AD、AB平行)
如图,小明同学在操场上的A处放风筝,风筝起飞后到达C处,此时,在AQ延长线上B处的小亮同学,发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上.已知旗杆PQ高为10m,若在B处测得旗杆顶点P的仰角为30°,A处测得点P
的仰角为45°,试求A、B之间的距离;此时,在A处又测得风筝的仰角为75°,若绳子AC在空中视为一条线段,绳子
AC的长约为多少?(结果可保留根号)
△ABC在直角坐标系中的位置如图所示,直线l经过点(-1,0),并且与y轴平行.
①将△ABC绕坐标原点O顺时针旋转90°得到△A1B1C1,在图中画出△A1B1C1;
②求出由点C运动到点C1所经过的路径的长.①△A2B2C2与△ABC关于直线l对称,画出△A2B2C2,并写出△A2B2C2三个顶点的
坐标;②观察△ABC与△A2B2C2对应点坐标之间的关系,写出直角坐标系中任意一点P(a,b)
关于直线l的对称点的坐标:__________.
如图,四边形ABCD内接于⊙O,BD是⊙O的直径, 于点E,DA平分
于点E,DA平分 .
. 试说明AE是⊙O的切线;
如果AB= 4,AE=2,求⊙O的半径.

如图①,将一张直角三角形纸片ABC折叠,使点A与点C重合,这时DE为折痕,△CBE为等腰三角形,再继续将纸片沿△CBE的对称轴EF折叠,这时得到了两个完全重合的矩形(其中一个是原三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样的两个矩形为“叠加矩形”.请完成下列问题:
如图②,正方形网格中的△ABC能折叠成“叠加矩形”吗?如能,请在图②中画出折痕;
如图③,在正方形网格中,以给定的BC为一边,画出一个斜△ABC,使其顶点A在格点上,且△ABC折成的“叠加矩形”为正方形;
如果一个三角形所折成的“叠加矩形” 为正方形,那么它必须满足的条件是 .

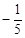

 ,则
,则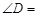
 中自变量x的取值范围是
中自变量x的取值范围是

 =
= 的图像在第一、三象限,则k的值可以是
的图像在第一、三象限,则k的值可以是 



 粤公网安备 44130202000953号
粤公网安备 44130202000953号