初中数学一次函数的最值解答题

钓鱼岛是我国渤海海峡上的一颗明珠，渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后，发现一外国舰艇进入我国水域向钓鱼岛驶来，渔船向渔政部门报告，并立即返航.渔政船接到报告后，立即从该港口出发赶往钓鱼岛.下图是渔船及渔政船与港口的距离s和渔船离开港口的时间t之间的函数图象.（假设渔船与渔政船沿同一航线航行）

（1）直接写出渔船离港口的距离s和它离开港口的时间t的函数关系式.]
（2）求渔船和渔政船相遇时，两船与钓鱼岛的距离.
（3）在渔政船驶往钓鱼岛的过程中，求渔船从港口出发经过多长时间与渔政船相距30海里？

写出一个实数k的值，使得正比例函数y=的图象在二、四象限．

阅读下面的材料：
在平面几何中，我们学过两条直线平行的定义．下面就两个一次函数的图象所确定的两条直线，给出它们平行的定义：设一次函数的图象为直线，一次函数的图象为直线，若，且，我们就称直线与直线互相平行．已知一次函数的图象为直线，过点且与已知直线平行的直线为。
解答下面的问题：
（1）求的函数表达式；
（2）设直线分别与轴、轴交于点A、B，过坐标原点O作OC⊥AB，垂足为C，求和两平行线之间的距离 ；
（3）若Q为OA上一动点，求QP+QB的最小值，并求取得最小值时Q点的坐标。
（4）在轴上找一点M，使△BMP为等腰三角形，求M的坐标。（直接写出答案）

为加强公民的节水意识，合理利用水资源．某市对居民用水实行阶梯水价，居民家庭每月用水量划分为三个阶梯，一、二、三级阶梯用水的单价之比等于1：1.5：2．如图折线表示实行阶梯水价后每月水费 $y$（元）与用水量 $x$m³之间的函数关系．其中线段AB表示第二级阶梯时 $y$与 $x$之间的函数关系.

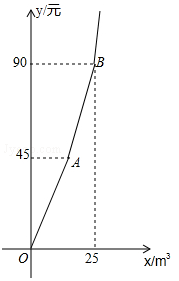
（1）写出点 $B$的实际意义；
（2）求线段 $AB$所在直线的表达式；
（3）某户5月份按照阶梯水价应缴水费102元，其相应用水量为多少立方米？

某家电生产企业根据市场调查分析，决定调整产品生产方案，准备每周（按120个工时计算）生产空调器、彩电、冰箱共360台，且冰箱至少生产60台，已知生产这些家电产品每台所需工时和每台产值如下表：

家电名称	空调	彩电	冰箱
工 时	1 2	1 3	1 4
产值（千元）	4	3	2

 
问每周应生产空调器、彩电、冰箱各多少台，才能使产值最高？最高产值是多少？（以千元为单位）

如图，函数的图象与函数（）的图象交于A（，1）B（1，）两点．

（1）求函数的表达式；    
（2）观察图象，比较当时，与的大小．

一个有进水管与出水管的容器，从某时刻开始4min内只进水不出水，在随后的8min内既进水又出水，每分的进水量和出水量有两个常数，容器内的水量y（单位：L）与时间x（单位：min）之间的关系如图所示．

（1）当4≤x≤12时，求y关于x的函数解析式；
（2）直接写出每分进水，出水各多少升．

开学初，小明到文具批发部一次性购买某种笔记本，该文具批发部规定：这种笔记本售价y（元/本）与购买数量x（本）之间的函数关系如图所示．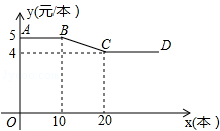

（1）图中线段AB所表示的实际意义是     ；
（2）请直接写出y与x之间的函数关系式；
（3）已知该文具批发部这种笔记本的进价是3元/本，若小明购买此种笔记本超过10本但不超过20本，那么小明购买多少本时，该文具批发部在这次买卖中所获的利润W（元）最大？最大利润是多少？

一农民带上若干千克自产的土豆进城出售，为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售，售出的土豆千克数与他手中持有的钱数（含备用零钱）的关系，如图所示，结合图象回答下列问题．

（1）农民自带的零钱是多少？
（2）试求降价前y与x之间的关系式？
（3）由表达式你能求出降价前每千克的土豆价格是多少？
（4）降价后他按每千克0．4元将剩余土豆售完，这时他手中的钱（含备用零钱）是26元，试问他一共带了多少千克土豆？

如图，正方形ABCD、正方形A₁B₁C₁D₁和正方形A₂B₂C₂D₂均位于平面直角坐标系的第一象限内，它们的边平行于x轴或y轴，其中点A，A₁，A₂在直线OM上，点C，C₁，C₂在直线ON上，O为坐标原点，已知点A的坐标为（3，3），正方形ABCD的边长为1．

（1）求直线ON的函数解析式；
（2）若点C₁的横坐标为4，求正方形A₁B₁C₁D₁的边长；
（3）若正方形A₂B₂C₂D₂的边长为m，则点B₂的坐标为                 ．（用含字母m的代数式表示．

为奖励在演讲比赛中获奖的同学，班主任派学习委员小明为获奖同学买奖品，要求每人一件．小明到文具店看了商品后，决定奖品在钢笔和笔记本中选择．如果买4个笔记本和2支钢笔，则需86元；如果买3个笔记本和1支钢笔，则需57元．
（1）求购买每个笔记本和钢笔分别为多少元？
（2）售货员提示，买钢笔有优惠，具体方法是：如果买钢笔超过10支，那么超出部分可以享受8折优惠，若买x（x＞0）支钢笔需要花y元，请你求出y与x的函数关系式；
（3）在（2）的条件下，小明决定买同一种奖品，数量超过10个，请帮小明判断买哪种奖品省钱．

小锋家有一块四边形形状的空地（如图，四边形ABCD），其中AD∥BC，BC=1.6m，AD=5.5m，CD=5.2m，∠C=90°，∠A=53°．小锋的爸爸想买一辆长4.9m，宽1.9m的汽车停放在这块空地上，让小锋算算是否可行．
小锋设计了两种方案，如图1和图2所示．

（1）请你通过计算说明小锋的两种设计方案是否合理；
（2）请你利用图3再设计一种有别于小锋的可行性方案，并说明理由．
（参考数据：sin53°=0.8，cos53°=0.6，tan53°=）

一次函数图象经过（3，8）和（5，12）两点，求一次函数解析式．

一个容器中有一个进水管和两个出水管，从某一时刻开始2min内只进水不出水，在随后的4min内开启了一个出水管，既进水又出水，每个出水管每分钟出水7.5L，每分钟的进水量和出水量保持不变，容器内的水量y（L）与时间x（min）之间的函数关系如图所示．

（1）求a的值；
（2）当2≤x≤6时，求y关于x的函数关系式；
（3）若在6min之后，两个出水管均开启，进水管关闭，请在图中补全函数图象．

某单位准备印刷一批书面材料，现有两个印刷厂可供选择，甲厂的费用分为制作费和印刷费两部分，乙厂直接按印刷数量收取印刷费．甲厂的费用y（千元）与书面材料数量x（千份）的关系见表：

书面材料数量x（千份）	0	1	2	3	4	5	6	.........
甲厂的印刷费用y（千元）	1	1.5	2	2.5	3	3.5	4	.........

乙厂的印刷费用y（千元）与书面材料数量x（千份）的函数关系图象如图所示．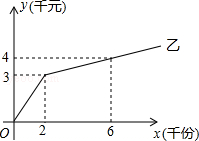

（1）请你写出甲厂的费用y与x的函数解析式，并在图中坐标系中画出甲厂的费用y与x的函数图象．
（2）请写出乙厂费用y与x的函数解析式，试求出当x在什么范围内时乙厂比甲厂的费用低？
（3）现有一客户需要印10千份书面材料，请问你如果是客户你如何选择？