某蔬菜加工厂承担出口蔬菜加工任务,有一批蔬菜产品需要装入某一规格的纸箱.供应这种纸箱有两种方案可供选择:
方案一:从纸箱厂定制购买,每个纸箱价格为4元;
方案二:由蔬菜加工厂租赁机器自己加工制作这种纸箱,机器租赁费按生产纸箱数收取.工厂需要一次性投入机器安装等费用16000元,每加工一个纸箱还需成本费2.4元.
(1)若需要这种规格的纸箱 个,请分别写出从纸箱厂购买纸箱的费用
个,请分别写出从纸箱厂购买纸箱的费用 (元)和蔬菜加工厂自己加工制作纸箱的费用
(元)和蔬菜加工厂自己加工制作纸箱的费用 (元)关于
(元)关于 (个)的函数关系式;
(个)的函数关系式;
(2)假设你是决策者,你认为应该选择哪种方案?并说明理由.
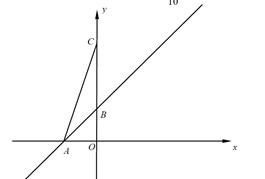
如图, 在平面直角坐标系中,AD=6,若OA、OB的长是关于x的一元二次方程
在平面直角坐标系中,AD=6,若OA、OB的长是关于x的一元二次方程 的两个根,且OA>OB.
的两个根,且OA>OB.
(1)求sin∠ABC的值.
(2)若E为x轴上的点,且 ,求经过D、E两点的直线的解析式,并判断△AOE与△DAO是否相似?
,求经过D、E两点的直线的解析式,并判断△AOE与△DAO是否相似?
(3)若点M在平面直角坐标系内,则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,请直接写出F点的坐标;若不存在,请说明理由.
已知⊙ 的半径为1,以
的半径为1,以 为原点,建立如图所示的直角坐标系.有一个正方形
为原点,建立如图所示的直角坐标系.有一个正方形 ,顶点
,顶点 的坐标为(
的坐标为( ,0),顶点
,0),顶点 在
在 轴上方,顶点
轴上方,顶点 在⊙
在⊙ 上运动.
上运动.
(1)当点 运动到与点
运动到与点 、
、 在一条直线上时,
在一条直线上时, 与⊙
与⊙ 相切吗?如果相切,请说明理由,并求出
相切吗?如果相切,请说明理由,并求出 所在直线对应的函数表达式;如果不相切,也请说明理由;
所在直线对应的函数表达式;如果不相切,也请说明理由;
(2)设点 的横坐标为
的横坐标为 ,正方形
,正方形 的面积为
的面积为 ,求出
,求出 与
与 的函数关系式,并求出
的函数关系式,并求出 的最大值和最小值.
的最大值和最小值.
国务院总理温家宝2011年11月16日主持召开国务院常务会议,会议决定建立青海三江源国家生态保护综合实验区。现要把228吨物资从某地运往青海甲、乙两地,用大、小两种货车共18辆,恰好能一次性运完这批物资。已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如下表:
| 运往地 车 型 |
甲 地(元/辆) |
乙 地(元/辆) |
| 大货车 |
720 |
800 |
| 小货车 |
500 |
650 |
(1)求这两种货车各用多少辆?
(2)如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为w元,求出w与a的函数关系式(写出自变量的取值范围);
(3)在(2)的条件下,若运往甲地的物资不少于120吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费。
如图,直线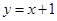 与
与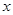 轴、
轴、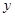 轴分别相交于点
轴分别相交于点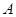 、
、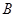 .抛物线
.抛物线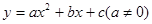 与
与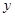 轴的正半轴相交于点
轴的正半轴相交于点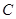 ,与这个一次函数的图像相交于
,与这个一次函数的图像相交于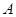 、
、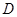 ,且
,且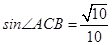 .
.
(1)求点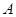 、
、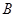 、
、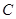 的坐标;
的坐标;
(2)如果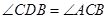 ,求抛物线
,求抛物线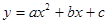 的解析式.
的解析式.
在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为 、
、 (km),
(km), 、
、 与x的函数关系如图所示.
与x的函数关系如图所示.
(1)填空:A、C两港口间的距离为 km, ;
;
(2)求图中点P的坐标,并解释该点坐标所表示的实际意义;
(3)甲、乙两船同在行驶途中,若两船距离不超过10 km时能够相互望见,求甲、乙两船可以相互望见时x的取值范围.
(1)证明:不论 取什么值,直线
取什么值,直线 :y=
:y= x-
x- 都通过一个定点;
都通过一个定点;
(2)以A(0,2)、B(2,0)、O(0,0)为顶点的三角形被直线 分成两部分,分别求出当
分成两部分,分别求出当 =2和
=2和 =-
=- 时,靠近原点O一侧的那部分面积.
时,靠近原点O一侧的那部分面积.
小明在上物理实验课时,利用量筒和体积相同的小球进行了如下操作:
请根据示意图中所给信息,解答下列问题:
(1)放入一个小球后,量筒中水面升高 cm;
(2)求放入小球后,量筒中水面的高度 (cm)与小球个数
(cm)与小球个数 (个)之间的函数关系式(不要求写出自变量的取值范围);
(个)之间的函数关系式(不要求写出自变量的取值范围);
(3)若往量筒中继续放入小球,量筒中的水就会溢出.问:量筒中至少放入几个小球时有水溢出?
小颖和小亮上山游玩,小颖乘会缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50 min才乘上缆车,缆车的平均速度为180 m/min.设小亮出发x min后行走的路程为y m.图中的折线表示小亮在整个行走过程中y与x的函数关系.
⑴小亮行走的总路程是____________㎝,他途中休息了________min.
⑵①当50≤x≤80时,求y与x的函数关系式;
②当小颖到达缆车终点为时,小亮离缆车终点的路程是多少?
小虎一家利用元旦三天驾车到某景点旅游,小汽车出发前油箱有油36L,匀速行驶若干小时后,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图象回答下列问题:
(1)求油箱余油量Q与行驶时间t之间的函数关系式;
(2)如果出发地距景点200km,车速为80km/h,要到达景点,油箱中的油是否够用?请说明理由.
如图,直线 与
与 轴负半轴、
轴负半轴、 轴正半轴分别交于A、B两点,正比例函数
轴正半轴分别交于A、B两点,正比例函数 的图像与直线AB交于点Q,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM =10,BN =3,
的图像与直线AB交于点Q,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM =10,BN =3,
(1)求A、B两点的坐标;(用b表示)
(2)图中有全等的三角形吗?若有,请找出并说明理由。
(3)求MN的长.
 、
、 两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往
两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往 城,乙车驶往
城,乙车驶往 城,甲车在行驶过程中速度始终不变.甲车距
城,甲车在行驶过程中速度始终不变.甲车距 城高速公路入口处的距离
城高速公路入口处的距离 (千米)与行驶时间
(千米)与行驶时间 (时)之间的关系如图.
(时)之间的关系如图.
(1)求 关于
关于 的表达式;
的表达式;
(2)已知乙车以60千米/时的速度匀速行驶,设行驶过程中,相遇前两车相距的路程为 (千米).请直接写出
(千米).请直接写出 关于
关于 的表达式;
的表达式;
(3)当乙车按(2)中的状态行驶与甲车相遇后,速度随即改为 (千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度
(千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度 .
.
已知:如图,在平面直角坐标系 中,直线AB分别与
中,直线AB分别与 轴交于点B、A,与反比例函数的图象分别交于点C、D,
轴交于点B、A,与反比例函数的图象分别交于点C、D, 轴于点E,
轴于点E, .
.
(1)求该反比例函数的解析式;
(2)求直线AB的解析式.
据媒体报道,近期“手足口病”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“手足口病”,对教室进行“薰药消毒”.已知药物在燃烧机释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示(即图中线段OA和双曲线在A点及其右侧的部分),根据图象所示信息,解答下列问题:
(1)写出从药物释放开始,y与x之间的函数关系式级自变量的取值范围;
(2)据测定,当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始,至少在多长时间内,师生不能进入教室?