如图,直线l:y=-x- 与坐标轴交于A,C两点,过A,O,C三点作⊙O1,点E为劣弧AO上一点,连接EC,EA,EO,当点E在劣弧AO上运动时(不与A,O两点重合),
与坐标轴交于A,C两点,过A,O,C三点作⊙O1,点E为劣弧AO上一点,连接EC,EA,EO,当点E在劣弧AO上运动时(不与A,O两点重合),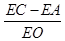 的值是否发生变化?( )
的值是否发生变化?( )
A. |
B.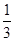 |
C.2 | D.变化 |

如图,在矩形ABCD中,O是对角线AC的中点,动点P,Q分别从点C,D出发,沿线段CB,DC方向匀速运动,已知P,Q两点同时出发,并同时到达终点B,C.连接OP,OQ.设运动时间为t,四边形OPCQ的面积为S,那么下列图象能大致刻画S与t之间的关系的是
在平面直角坐标系内,直线y=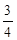 x+3与两坐标轴交于A、B两点,点O为坐标原点,若在该坐标平面内有以点P(不与点A、B、O重合)为顶点的直角三角形与Rt△ABO全等,且这个以点P为顶点的直角三角形与Rt△ABO有一条公共边,则所有符合条件的P点个数为( )
x+3与两坐标轴交于A、B两点,点O为坐标原点,若在该坐标平面内有以点P(不与点A、B、O重合)为顶点的直角三角形与Rt△ABO全等,且这个以点P为顶点的直角三角形与Rt△ABO有一条公共边,则所有符合条件的P点个数为( )
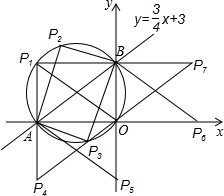
A.9个 B.7个 C.5个 D.3个
函数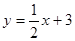 的图象与x、y轴分别交于点A、B,点P
的图象与x、y轴分别交于点A、B,点P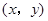 为直线AB上的一动点(
为直线AB上的一动点(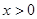 )过P作PC
)过P作PC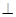 y轴于点C,若使
y轴于点C,若使 的面积大于
的面积大于 的面积,则P的横坐标x的取值范围是( )
的面积,则P的横坐标x的取值范围是( )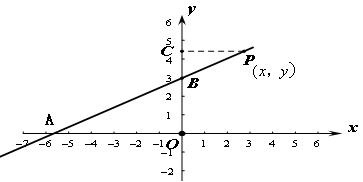
A、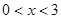 B、
B、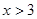 C、
C、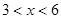 D、
D、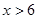
如图1,在直角梯形ABCD中,动点P从点B出发,沿BC,CD运动至点D停止.设点P运动的路程为 ,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是( )
| A.3 | B.4 | C.5 | D.6 |
在平面直角坐标系中,直线l:y=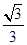 x+1交x轴于点A,交y轴于点B,点A1、A2、A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A1,△A1B2A2,△A2B3A3,…均为等边三角形,则△A5B6A6的周长是( )
x+1交x轴于点A,交y轴于点B,点A1、A2、A3,…在x轴上,点B1、B2、B3,…在直线l上.若△OB1A1,△A1B2A2,△A2B3A3,…均为等边三角形,则△A5B6A6的周长是( )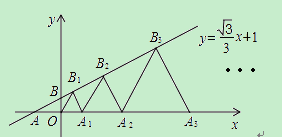
A.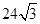 |
B.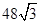 |
C.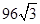 |
D.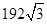 |
如图,函数y=-kx(k 与
与 的图象交于A、B两点,过A作AC
的图象交于A、B两点,过A作AC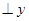 轴于C,则
轴于C,则 BOC的面积是( ).
BOC的面积是( ).
A.8 B .4 C. 2 D.1
如图,正方形ABCD的边长为4,P为正方形边上一动点,沿A→D→C→B→A 的路径匀速移动,设P点经过的路径长为x,△APD的面积是y,则下列图象能大致反映y与x的函数关系的是
A. |
B. |
C. |
D. |
如图,一次函数y=ax+b与x轴,y轴交于A,B两点,与反比例函数y= 相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE,EF.有下列四个结论:①△CEF与△DEF的面积相等;②△AOB∽△FOE;③△DCE≌△CDF;④AC=BD.其中正确的结论个数是( )
相交于C,D两点,分别过C,D两点作y轴,x轴的垂线,垂足为E,F,连接CF,DE,EF.有下列四个结论:①△CEF与△DEF的面积相等;②△AOB∽△FOE;③△DCE≌△CDF;④AC=BD.其中正确的结论个数是( )
A.1 B.2 C.3 D.4
如图,直线 ,点
,点 坐标为(1,0),过点
坐标为(1,0),过点 作
作 轴的垂线交直线于点
轴的垂线交直线于点 B,以原点O为圆心,
B,以原点O为圆心, 长为半径画弧交
长为半径画弧交 轴于点
轴于点 ;再过点
;再过点 作
作 的垂线交直线于点
的垂线交直线于点 ,以原点O为圆心,
,以原点O为圆心, 长为半径画弧交
长为半径画弧交 轴于点
轴于点 ,…,按此做法进行下去,点
,…,按此做法进行下去,点 的坐标为( ).
的坐标为( ).
A. |
B. |
C. |
D. |

在数-1,1,2中任取两个数作为点坐标,那么该点刚好在一次函数 图象上的概率是( )
图象上的概率是( )
A.  |
B. |
C. |
D. |
如图,AB是半圆O的直径,点P从点O出发,沿线段OA—弧AB—线段OB的路径运动一周.设 为
为 ,运动时间为
,运动时间为 ,则下列图形能大致地刻画
,则下列图形能大致地刻画 与
与 之间关系的是( )
之间关系的是( )
如图,在直角梯形 中,AB∥CD;
中,AB∥CD; ⊥
⊥ 动点
动点 从点
从点 出发,沿
出发,沿 ,
, 运动至点
运动至点 停止.设点
停止.设点 运动的路程为
运动的路程为 ,
, 的面积为
的面积为 ,如果
,如果 关于
关于 的函数图象如图所示,则
的函数图象如图所示,则 的面积是( )
的面积是( )
| A.3 | B.4 | C.5 | D.6 |
