初中数学一次函数的最值选择题

平行四边形的周长为240，两邻边长为x、y，则y与x之间的关系是（ ）

A．y=120﹣x（0＜x＜120）

B．y=120﹣x（0≤x≤120）

C．y=240﹣x（0＜x＜240）

D．y=240﹣x（0≤x≤240）

一次测验中的填空题如下：
（1）当m取1时，一次函数y=（m﹣2）x+3的图象，y随x的增大而 增大   ；
（2）等腰梯形ABCD，上底AD=2，下底BC=8，∠B=60°，则腰长AB= 6  ；
（3）菱形的边长为6cm，一组相邻角的比为1：2，则菱形的两条对角线的长分别为  6cm和cm  ；
（4）如果一个多边形的内角和为900°，则这个多边形是 五  边形；
你认为正确的添空个数是（ ）

A．1

B．2

C．3

D．4

已知一次函数y＝kx－1，若y随x的增大而增大，则它的图象经过（      ）

A．第一、二、三象限	B．第一、二、四象限
C．第一、三、四象限	D．第二、三、四象限

小明从家出发，外出散步，到一个公共阅报栏前看了一会报后，继续散步了一段时间，然后回家，如图描述了小明在散步过程汇总离家的距离s（米）与散步所用时间t之间的函数关系，根据图象，下列信息错误的是（ ）

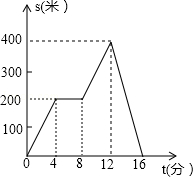
A．小明看报用时8分钟

B．公共阅报栏距小明家200米

C．小明离家最远的距离为400米

D．小明从出发到回家共用时16分钟

若关于x，y的二元一次方程组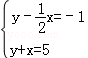的解是，则直线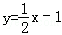与y=﹣x+5的交点坐标为（ ）

A．（4，1）

B．（1，4）

C．（﹣4，1）

D．（2，1）

已知一次函数y=（m+1）x+m²﹣1（m为常数），若它的图象过原点，则（ ）

A．m=1

B．m=±1

C．m=﹣1

D．m=0

老王以每千克0．8元的价格从批发市场购进若干千克西瓜到市场销售，在销售了部分西瓜后，余下的每千克降价0．2元，全部售完，销售金额与卖瓜的千克数之间的关系如图所示，那么老王赚了（  ）

A．32元

B．36元

C．38元

D．44元

一次函数y=kx+b，经过（1，1），（2，﹣4），则k与b的值为（ ）

A．

B．

C．

D．

P₁（x₁，y₁），P₂（x₂，y₂）是正比例函数图象上的两点，下列判断中，正确的是（   ）

A．y1＞y2

B．y1＜y2

C．当x1＜x2时，y1＜y2

D．当x1＜x2时，y1＞y2

小高从家门口骑车去单位上班，先走平路到达点A，再走上坡路到达点B，最后走下坡路到达工作单位，所用的时间与路程的关系如图所示．下班后，如果他沿原路返回，且走平路、上坡路、下坡路的速度分别保持和去上班时一致，那么他从单位到家门口需要的时间是（ ）

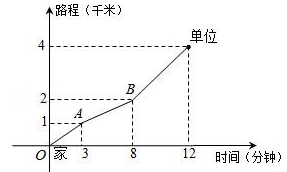
A．12分钟

B．15分钟

C．25分钟

D．27分钟

如果y=（m﹣2）+2是一次函数，那么m的值是（ ）

A．2

B．﹣2

C．±2

D．

如图，过A点的一次函数的图象与正比例函数y=2x的图象相交于点B，则这个一次函数的解析式是（ ）

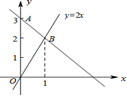
A．y=2x+3

B．y=x﹣3

C．y=2x﹣3

D．y=﹣x+3

向最大容量为60升的热水器内注水，每分钟注水10升，注水2分钟后停止注水1分钟，然后继续注水，直至注满．则能反映注水量与注水时间函数关系的图象是（ ）

A．	B．
C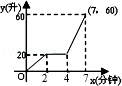．	D．

有一天早上，小刚骑车上学，途中用了10 min吃早餐，用完早餐后，小刚发现如果按原来速度上学会迟到，于是他加快了骑车速度，终于在上课前到达学校，下面几个图形中能大致反映小刚上学过程中路程与时间关系的图象是            （   ）

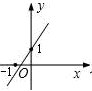
已知函数y=kx+b的图象如图，则y=2kx+b的图象可能是（ ）