初中数学一次函数的最值选择题

在同一直角坐标系中，一次函数和二次函数的图象大致为 （     ）

一次函数y=kx+b（k≠0）的图象如图所示，当y＞0时，x的取值范围是（ ）

A．x＜0

B．x＞0

C．x＜2

D．x＞2

如图（1），在Rt△ABC中，∠ACB=90°，D是斜边AB的中点，动点P从B点出发，沿B→C→A运动，设S_△DPB=y，点P运动的路程为x，若y与x之间的函数图象如图（2）所示，则△ABC的面积为（ ）

A．4

B．6

C．12

D．14

如图，点A的坐标为（-2，0），点B在直线y=x上运动，当线段AB最短时，点B的坐标为（     ）

A．（，）

B．（，）

C．（0，0）

D．（-1，-1）

若正比例函数y=mx（m≠0），y随x的增大而减小，则它和二次函数y=mx²+m的图象大致是（  ）

小亮家与学校相距1500m，一天放学后他步行回家，最初以某一速度匀速前进，途中遇到熟人小强，说话耽误了几分钟，与小强告别后他就改为匀速慢跑，最后回答了家，设小亮从学校出发后所用的时间为t（min），与家的距离为s（m），下列图象中，能表示上述过程的是（     ）

时钟在正常运行时，时针和分针的夹角会随着时间的变换而变化，设时针与分针的夹角为y度，运行时间为t分，当时间从3：00开始到3：30止，图中能大致表示y与t之间的函数关系的图象是（ ）

已知A、B两地相距120千米，甲骑自行车以20千米/时的速度由起点A前往终点B，乙骑摩托车以40千米/时的速度由起点B前往终点A．两人同时出发，各自到达终点后停止．设两人之间的距离为s（千米），甲行驶的时间为t（小时），则下图中正确反映s与t之间函数关系的是

如果y=（m﹣2）+2是一次函数，那么m的值是（ ）

A．2

B．﹣2

C．±2

D．

如图，过A点的一次函数的图象与正比例函数y=2x的图象相交于点B，则这个一次函数的解析式是（ ）

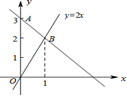
A．y=2x+3

B．y=x﹣3

C．y=2x﹣3

D．y=﹣x+3

向最大容量为60升的热水器内注水，每分钟注水10升，注水2分钟后停止注水1分钟，然后继续注水，直至注满．则能反映注水量与注水时间函数关系的图象是（ ）

A．	B．
C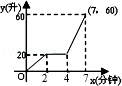．	D．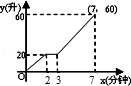

有一天早上，小刚骑车上学，途中用了10 min吃早餐，用完早餐后，小刚发现如果按原来速度上学会迟到，于是他加快了骑车速度，终于在上课前到达学校，下面几个图形中能大致反映小刚上学过程中路程与时间关系的图象是            （   ）

已知函数y=kx+b的图象如图，则y=2kx+b的图象可能是（ ）

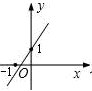
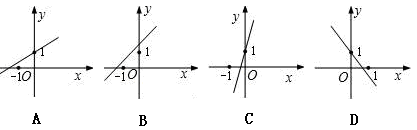
在同一坐标系中，正比例函数y=kx与一次函数y=x－k的图象为（   ）

已知一次函数y=kx+b的图象经过第一、二、三象限，则b的值可以是（   ）．

A．﹣2

B．﹣1

C．0

D．2