初中数学一次函数的最值试题

如图，A（0，1），M（3，2），N（4，4） , 动点P从点A出发，沿y
轴以每秒1个单位长的速度向上移动，且过点P的直线l：y＝－x+b也随之移动，设移动时间为 t 秒.（直线y = kx+b平移时k不变）

（1）当t＝3时，求 l 的解析式；
（2）若点M，N位于l 的异侧，确定 t 的取值范围.

某地出租车计费方法如图所示，x（km）表示行驶里程，y（元）表示车费，请根据图像解答下列问题：

（1）该地出租车的起步价是多少元？
（2）当x＞2时，求y与x之间的函数关系式；
（3）若某乘客有一次乘出租车的里程为18km，则这位乘客需付出租车车费多少元？

甲、乙两辆摩托车同时从相距20km的A、B两地出发，相向而行，图中分别表示甲、乙两辆摩托车到A地的距离s（km）与行驶时间t（h）的函数关系，则下列说法错误的是（   ）．

A．乙摩托车的速度较快
B．经过0．3小时甲摩托车行驶到A、B两地的中点
C．经过0．25小时两摩托车相遇
D．当乙摩托车到达A地时，甲摩托车距离A地km．

如图反映的过程是：矩形中，动点从点出发，依次沿对角线、边、边运动至点停止，设点的运动路程为， ．则矩形的周长是

A．6

B．12

C．14

D．15

如图，已知A（-4，2）、B（n，-4）是一次函数y=kx+b的图象与反比例函数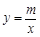 的图象的两个交点．

（1）求此反比例函数和一次函数的解析式；
（2）根据图象写出使一次函数的值小于反比例函数的值的x的取值范围．

为了鼓励送彩电下乡，国家决定对购买彩电的农户实行政府补贴．规定每购买一台彩电，政府补贴若干元，经调查某商场销售彩电台数y（台）与补贴款额x（元）之间大致满足如图①所示的一次函数关系．随着补贴款额x的不断增大，销售量也不断增加，但每台彩电的收益Z（元）会相应降低且Z与x之间也大致满足如图②所示的一次函数关系。

（1）在政府未出台补贴措施前，该商场销售彩电的总收益额为多少元？
（2）在政府补贴政策实施后，分别求出该商场销售彩电台数y和每台家电的收益z与政府补贴款额x之间的函数关系式；
（3）要使该商场销售彩电的总收益w（元）最大，政府应将每台补贴款额x定为多少并求出总收益w的最大值。

小芳步行上学，最初以某一速度匀速前进，中途遇红灯，稍作停留后加快速度跑步去上学，到校后，她请同学们画出她行进路程s（米）与行进时间t（分钟）的函数图象的示意图.你认为正确的是（   ）

已知过原点O的两直线与圆心为M（0，4），半径为2的圆相切，切点分别为P、Q，PQ交y轴于点K，抛物线经过P、Q两点，顶点为N（0，6），且与x轴交于A、B两点．

（1）求点P的坐标；
（2）求抛物线解析式；
（3）在直线y=nx+m中，当n=0，m≠0时，y=m是平行于x轴的直线，设直线y=m与抛物线相交于点C、D，当该直线与⊙M相切时，求点A、B、C、D围成的多边形的面积（结果保留根号）．

某公司投资700万元购买甲、乙两种产品的生产技术和设备后,进行这两种产品的生产加工.已知生产甲种产品每件还需成本费30元,生产乙种产品每件还需成本费20元.经市场调研发现:甲种产品的销售单价定在35元到70元之间较为合理,设甲种产品的销售单价为x（元）,年销售量为y（万件）.当35≤x≤50时,y与x之间的函数关系式为y=20－0.2x;当50≤x≤70时,y与x之间的函数关系如图所示.乙种产品的销售单价在25元（含）到45元（含）之间,且年销售量稳定在10万件.物价部门规定这两种产品的销售单价之和为90元.
 
（1）当50≤x≤70时,求出甲种产品的年销售量y（万件）与x（元）之间的函数解析式.
（2）若该公司第一年的年销售利润（年销售利润=年销售收入－生产成本）为W（万元）,那么怎样定价,可使第一年的年销售利润最大?最大年销售利润是多少?
（3）第二年公司可重新对产品进行定价,在（2）的条件下,并要求甲种产品的销售单价x（元）在50≤x≤70范围内,该公司希望到第二年年底,两年的总盈利（总盈利=两年的年销售利润之和－投资成本）不低于85万元.请求出第二年乙种产品的销售单价m（元）的范围.

某地方政府出台了一系列“三农”优惠政策，使农民收入大幅度增加。某农户生产经销一种农产品，已知这种产品的成本价为每千克20元，市场调查发现，该产品每天的销售量y（千克）与销售价x（元/千克）有如下关系：y=-2x+80。设这种产品每天的销售利润为W元。
（1）求W与x之间的函数关系式。
（2）该产品销售价定为每千克多少元时，每天的销售利润最大？最大利润是多少元？
（3）如果物价部门规定这种产品的销售价不高于每千克28元，该农户想要每天获得150元的销售利润，销售价应定为每千克多少元？

机械加工需要用油进行润滑以减小摩擦，某企业加工一台大型机械设备润滑用油量为90千克，用油的重复利用率为60%，按此计算，加工一台大型机械设备的实际耗油量为36千克，为了建设节约型社会，减少油耗，该企业的甲、乙两个车间都组织了人员为减少实际耗油量进行攻关.（1）甲车间通过技术革新后，加工一台大型机械设备润滑用油量下降到70千克，用油量的重复利用率仍然为60%.问甲车间技术革新后，加工一台大型机械设备的实际耗油量是多少千克？
（2）乙车间通过技术革新后，不仅降低了润滑用油量，同时也提高了用油的重复利用率，并且发现在技术革新前的基础上，润滑用油量每减少1千克，用油的重复利用率将增加1.6%，这样乙车间加工一台大型机械设备的实际耗油量下降到12千克，问乙车间技术革新后，加工一台大型机械设备的润滑用油量是多少千克？用油的重复利用率是多少？

（1）在遇到问题：“钟面上，如果把时针与分针看作是同一平面内的两条线段，在2∶00~2∶15之间，时针与分针重合的时刻是多少？”时，小明尝试运用建立函数关系的方法：

①恰当选取变量x和y．小明设2点钟之后经过x min（0≤x≤15），时针、分针分别与竖轴线（即经过表示“12”和“6”的点的直线，如图1）所成的角的度数为y₁°、y₂°；
②确定函数关系．由于时针、分针在单位时间内转动的角度不变，因此既可以直接写出y₁、y₂关于x的函数关系式，也可以画出它们的图象．小明选择了后者，画出了图2；
③根据题目的要求，利用函数求解．本题中小明认为求出两个图象交点的横坐标就可以解决问题．
（2）请运用建立函数关系的方法解决问题：钟面上，如果把时针与分针看作是同一平面内的两条线段，在7∶30~8∶00之间，时针与分针互相垂直的时刻是多少？（请你按照小明的思路解决这个问题．）

某电视机生产厂家去年销往农村的某品牌电视机每台的售价y（元）与月份x之间满足函数关系，去年的月销售量p（万台）与月份x之间成一次函数关系，其中两个月的销售情况如下表：

（1）求p与x之间的一次函数关系．
（2）求该品牌电视机在去年哪个月销往农村的销售金额最大？最大是多少？
（3）由于受国际金融危机的影响，今年1、2月份该品牌电视机销往农村的售价都比去年12月份下降了，且每月的销售量都比去年12月份下降了。国家实施“家电下乡”政策，即对农村家庭购买新的家电产品，国家按该产品售价的13%给予财政补贴。受此政策的影响，今年3月份至5月份，该厂家销往农村的这种电视机在保持今年2月份的售价不变的情况下，平均每月的销售量比今年2月份增加了1.5万台。若今年3至5月份国家对这种电视机的销售共给予财政补贴936万元，求的值（保留一位小数）
（参考数据：，，， 销售金额=售价销售量）

从﹣1，1，2这三个数字中，随机抽取一个数，记为a，那么，使关于x的一次函数y=2x+a的图象与x轴、y轴围成的三角形的面积为，且使关于x的不等式组有解的概率为__ ．

（本小题满分10分）某公司研制出一种新颖的家用小电器，每件的生产成本为18元，经市场调研表明，按定价40元出售，每日可销售20件．为了增加销量，每降价1元，日销售量可增加2件．问将售价定为多少元时，才能使日利润最大？求最大利润．