初中数学一次函数的最值试题

直线与的位置关系为           ．

一名考生步行前往考场， 10分钟走了总路程的1/4，估计步行不能准时到达，于是他改乘出租车赶往考场，他的行程与时间关系如图所示（假定总路程为1），则他到达考场所花的时间比一直步行提前了（       ）

A．20分钟

B．22分钟

C．24分钟

D．26分钟

已知P1（﹣1，y1），P2（2，y2）是一次函数y=﹣x+3的图象上的两点，则y1      y2（填“＞”或“＜”或“=”）．

一次函数的图象过点（﹣1，0），且函数值随着自变量的增大而减小，写出一个符合这个条件的一次函数解析式：      ．（答案不唯一）

已知函数y=kx+b的图象如图所示，则一元二次方程x²+x+k-1=0根的存在情况是（ ）

A．没有实数根

B．有两个相等的实数根

C．有两个不相等的实数根

D．无法确定

已知直线，它与坐标轴围成的三角形的面积为（   ）

A．6

B．10

C．25

D．30

下列命题是真命题的是（ ）

A．同位角相等

B．平行于同一直线的两条直线平行

C．点（2，3）在直线y=2x+3上

D．函数y=﹣x+1中y随x的增大而增大

如图，直线l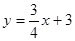：  交x、y轴分别为A、B两点，C点与A点关于y轴对称．动点P、Q分别在线段AC、AB上（点P不与点A、C重合），满足∠BPQ=∠BAO．

（1）点A坐标是__________，点B的坐标__________，BC=__________．
（2）当点P在什么位置时，△APQ≌△CBP，说明理由．
（3）当△PQB为等腰三角形时，求点P的坐标．

利用图象解方程组．

在同一直角坐标系中，一次函数y=kx-k与反比例函数的图象大致是（    ）

某书定价25元，如果一次购买20本以上，超过20本的部分打八折，试写出付款金额y（单位：元）与购书数量x（单位：本）之间的函数关系          ．

将直线y=3x+1平移向下平移4个单位，则平移后的解析式为      ．

过点P（8，2）且与直线y=x+1平行的一次函数解析式为_________．

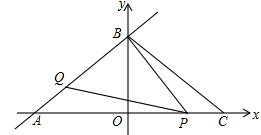
某气球内充满一定质量的气体，当温度不变时，气球内气体的气压p（kPa）是气体体积V（m³）的反比例函数，其图象如图所示．

（1）写出这一函数的表达式．
（2）当气体体积为1 m³时，气压是多少？
（3）当气球内的气压大于140 kPa时，气球将爆炸，为了安全考虑，气体的体积应不小于多少？

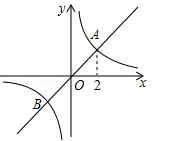
如图，正比例函数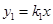的图象与反比例函数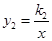的图象相交于A，B两点，其中点A的横坐标为2，当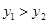时，x的取值范围是（ ）

A．x＜﹣2或x＞2

B．x＜﹣2或0＜x＜2

C．﹣2＜x＜0或0＜x＜﹣2

D．﹣2＜x＜0或x＞2