初中数学一次函数的最值试题

直线y=4x-2与两坐标轴围成的三角形的面积是                 ．

一根蜡烛长20cm，点燃后每小时燃烧5cm，燃烧时剩下的高度h（单位：cm）与燃烧时间t（单位：h）（0≤t≤4）之间的关系是                ．

已知函数y=（m-3）x+1-2m是正比例函数，则m=            ．

下列函数（1）y=3πx；（2）y=8x-6；（3）y=；（4）y=-8x；（5）y=5x²-4x+1中，是一次函数的有（ ）

A．4个

B．3个

C．2个

D．1个

已知一次函数y=-x+3，当0≤x≤2时，y的最大值是                ．

若一次函数y=（m﹣3）x+5的函数值y随x的增大而增大，则（ ）

A．m＞0

B．m＜0

C．m＞3

D．m＜3

已知一次函数y=（﹣3a+1）x+a的图象上两点A（x₁，y₁），B（x₂，y₂），当x₁＞x₂时，y₁＞y₂，且图象不经过第四象限，则a的取值范围是            ．

在同一坐标系中，函数y=和y=kx+3（k≠0）的图象大致是（ ）

直线y=x+3与x轴的交点是（）

A．（﹣3，0）

B．（0，﹣3）

C．（0，3）

D．（3，0）

甲、乙两商场春节期间都进行让利酬宾活动．其中，甲商场对一次购物中超过200元后的价格部分打7折，如图所示，表示甲商场在让利方式下y关于x的函数图象，x（单位：元）表示商品原价，y（单位：元）表示购物金额．若乙商场所有商品按8折出售，请在同一坐标系下画出乙商场在让利方式下y关于x的函数图象，并说明如何选择这两家商场购物更省钱．

以下四点：（1，2），（2，3），（0，1），（﹣2，3）在直线y=2x+1上的有（ ）

A．1个

B．2个

C．3个

D．4个

下列各式中，y随x的变化关系式是正比例函数的是（ ）

A．y="2x"

B．y=

C．y=x﹣1

D．y=x^2﹣1

如图，在平面直角坐标系中，线段AB的端点坐标为A（﹣2，4），B（4，2），直线y=kx﹣2与线段AB有交点，请写出一个k的可能的值              ．

（1）根据画函数图象的步骤，在如图的直角坐标系中，画出函数y=|x|的图象；
（2）求证：无论m取何值，函数y=mx﹣2（m﹣1）的图象经过的一个确定的点；
（3）若（1），（2）中两图象围成图形的面积刚好为2，求m值．

已知一次函数y=kx+b的图象（如图），当x＜0时，y的取值范围是（   ）

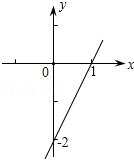
A．y＞0

B．y＜0

C．﹣2＜y＜0

D．y＜﹣2