如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
(1)当BC=1时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;
(3)设BD=x,△DOE的面积为y,求y关于x的函数关系式,并写出它的定义域.
如图,在平面直角坐标系中,二次函数y=ax2+6x+c的图象经过点A(4,0)、B(﹣1,0),与y轴交于点C,点D在线段OC上,OD=t,点E在第二象限,∠ADE=90°,tan∠DAE= ,EF⊥OD,垂足为F.
,EF⊥OD,垂足为F.
(1)求这个二次函数的解析式;
(2)求线段EF、OF的长(用含t的代数式表示);
(3)当∠ECA=∠OAC时,求t的值.
(图文不相符)
如图,点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.
(1)求点B的坐标;
(2)求经过点A.O、B的抛物线的解析式;
(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,说明理由.

如图,以OA1=2为底边做等腰三角形,使得第三个顶点C1恰好在直线y=x+2上,并以此向左、右依次类推,作一系列底边为2,第三个顶点在直线y=x+2上的等腰三角形.
(1)请你通过计算说明:底边为2,顶点在直线y=x+2上且面积为21的等腰三角形位于图
中什么位置?
(2)求证:y轴右侧的每一个等腰三角形的面积都等于前后两个以腰为一边的三角形面积之和的一半(如:S右1= ,S右2=
,S右2= ).
).
(3)过D1、A1、C2三点画抛物线.问在抛物线上是否存在点P,使得△PD1C2的面积是△C1OD1与△C1A1C2面积和的 .若存在,请求出点P的坐标;若不存在,请说明理由.
.若存在,请求出点P的坐标;若不存在,请说明理由.
如图①,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在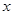 轴的正半轴上,点C在
轴的正半轴上,点C在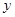 轴的正半轴上,OA=5,OC=4.
轴的正半轴上,OA=5,OC=4.
(1)在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D、E两点的坐标;
(2)如图②,若AE上有一动点P(不与A、E重合)自A点沿AE方向向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为秒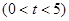 ,过P点作ED的平行线交AD于点M,过点M作AE的平行线交DE于点N.求四边形PMNE的面积S与时间之间的函数关系式;当取何值时,S有最大值?最大值是多少?
,过P点作ED的平行线交AD于点M,过点M作AE的平行线交DE于点N.求四边形PMNE的面积S与时间之间的函数关系式;当取何值时,S有最大值?最大值是多少?
(3)在(2)的条件下,当为何值时,以A、M、E为顶点的三角形为等腰三角形,并求出相应时刻点M的坐标.
如图, 已知直线 分别与
分别与 轴,
轴,  轴交于
轴交于 两点, 点
两点, 点 在
在 轴上. 以点
轴上. 以点 为圆心的⊙
为圆心的⊙ 与直线
与直线 相切于点
相切于点 , 连接
, 连接 .
.
(1) 求证:  ∽
∽ ;
;
(2)如果⊙ 的半径为
的半径为 , 求出点
, 求出点 的坐标, 并写出以
的坐标, 并写出以 为顶点, 且过点
为顶点, 且过点 的抛物线的解析式;
的抛物线的解析式;
(3) 在(2)的条件下, 在此抛物线上是否存在点 , 使得以
, 使得以 三点为顶点的三角形与
三点为顶点的三角形与 相似? 如果存在, 请求出所有符合条件的点
相似? 如果存在, 请求出所有符合条件的点 的坐标; 如果不存在, 请说明理由.
的坐标; 如果不存在, 请说明理由.
在平面直角坐标系xOy中,抛物线y= - x2+
x2+ x+m2-3m+2 与x轴的交点分别为原点O和点A,点B(2,n)在这条抛物线上。
x+m2-3m+2 与x轴的交点分别为原点O和点A,点B(2,n)在这条抛物线上。

(1) 求点B的坐标;
(2) 点P在线段OA上,从O点出发向A点运动,过P点作x轴的垂线,与直线OB交于点E。延长PE到点D。使得ED=PE。 以PD为斜边在PD右侧作等腰直角三角形PCD(当P点运动时,C点、D点也随之运动)
j当等腰直角三角形PCD的顶点C落在此抛物线上时,求OP的长;
k若P点从O点出发向A点作匀速运动,速度为每秒1个单位,同时线段OA上另一点Q从A点出发向O点作匀速运动,速度为每秒2个单位(当Q点到达O点时停止运动,P点也同时停止运动)。过Q点作x轴的垂线,与直线AB交于点F。延长QF到点M,使得FM=QF,以QM为斜边,在QM的左侧作等腰直角三角形QMN(当Q点运动时,M点,N点也随之运动)。若P点运动到t秒时,两个等腰直角三角形分别有一条直角边恰好落在同一条直线上,求此刻t的值。
如图1,已知矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3;抛物线 经过坐标原点O和x轴上另一点E(4,0)
经过坐标原点O和x轴上另一点E(4,0)
图1 图2
(1)当x取何值时,该抛物线的最大值是多少?
(2)将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀速移动.设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图2所示).
① 当 时,判断点P是否在直线ME上,并说明理由;
时,判断点P是否在直线ME上,并说明理由;
② 以P、N、C、D为顶点的多边形面积是否可能为5,若有可能,求出此时N点的坐标;若无可能,请说明理由.
在平面直角坐标系中,抛物线y=ax2+bx+2的图象过 和
和 ,与
,与 轴交于点
轴交于点 ,与
,与 轴交于另一点
轴交于另一点 ,点
,点 是原点
是原点 关于点
关于点 的对称点,连结
的对称点,连结 、
、 ,设点
,设点 。
。
(1)求抛物线的解析式;
(2)连结 、
、 ,①求
,①求 的值;②将
的值;②将 绕点
绕点 旋转,在旋转过程中如图(2),线段
旋转,在旋转过程中如图(2),线段 和
和 的比值会变吗?请说明理由;
的比值会变吗?请说明理由;
(3)设点 是直线
是直线 上方的抛物线上一点,连结
上方的抛物线上一点,连结 ,以
,以 为边作图示一侧的正方形,随着点
为边作图示一侧的正方形,随着点 的运动,正方形的大小,位置也随之改变,当顶点
的运动,正方形的大小,位置也随之改变,当顶点 或
或 恰好落在
恰好落在 轴上时,直接写出对应点
轴上时,直接写出对应点 的坐标。
的坐标。
已知抛物线y=ax2+bx+c ,当x=0时,有最小值为1 ;且在直线y=2上截得的线段长为4 .
(1)求此抛物线的解析式;
(2)若点P是抛物线的任意一点,记点P到X轴的距离为d1,点P 与点 F (0,2)的距离为d 2 ,猜想d1、 d 2的大小关系,并证明;
(3)若直线PF交此抛物线于另一点Q(异于P点)。 试判断以PQ为直径的圆与x 轴的位置关系,并说明理由。
已知二次函数 :
:
(1) 证明:当m为整数时,抛物线 与x轴交点的横坐标均为整数;
与x轴交点的横坐标均为整数;
(2) 以抛物线 的顶点A为等腰Rt△的直角顶点,作该抛物线的内接等腰Rt△ABC(B、C两点在抛物线上),求Rt△ABC的面积(图中给出的是m取某一值时的示意图);
的顶点A为等腰Rt△的直角顶点,作该抛物线的内接等腰Rt△ABC(B、C两点在抛物线上),求Rt△ABC的面积(图中给出的是m取某一值时的示意图);
(3) 若抛物线 与直线y=7交点的横坐标均为整数,求整数m的值.
与直线y=7交点的横坐标均为整数,求整数m的值.
已知抛物线 交y轴于点A,交x轴于点B,C(点B在点C的右侧).过点A作垂直于y轴的直线l. 在位于直线l下方的抛物线上任取一点P,过点P作直线PQ平行于y轴交直线l于点Q.连接AP.
交y轴于点A,交x轴于点B,C(点B在点C的右侧).过点A作垂直于y轴的直线l. 在位于直线l下方的抛物线上任取一点P,过点P作直线PQ平行于y轴交直线l于点Q.连接AP.
(1)写出A,B,C三点的坐标;
(2)若点P位于抛物线的对称轴的右侧:
①如果以A,P,Q三点构成的三角形与△AOC相似,求出点P的坐标;
②若将△APQ沿AP对折,点Q的对应点为点M.是否存在点P,使得点M落在x轴上.若存在,求出点P的坐标;若不存在,请说明理由.
如图,已知抛物线y=ax +bx+c经过A(-3,0)、B(1,0)、C(0,3)三点,求:(1)抛物线解析式
+bx+c经过A(-3,0)、B(1,0)、C(0,3)三点,求:(1)抛物线解析式
(2)若抛物线的顶点为P,求∠PAC的正切值
(3)若以点A、C、P、M为顶点的四边形是平行四边形,求点M的坐标
如图,在平面直角坐标系中放置一直角三角板,其顶点为A(0,1),B(2,0),O(0,0),将此三角板绕原点O逆时针旋转90°,得到△A′B′O.
(1)一抛物线经过点A′、B′、B,求该抛物线的解析式;
(2)设点P是在第一象限内抛物线上的一动点,是否存在点P,使四边形PB′A′B的面积是△A′B′O面积4倍?若存在,请求出P的坐标;若不存在,请说明理由.
(3)在(2)的条件下,试指出四边形PB′A′B是哪种形状的四边形?并写出四边形PB′A′B的两条性质.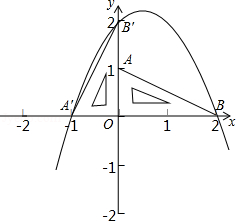
已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.