[浙江]2012届浙江省杭州市拱墅区中考模拟(二)数学试卷
如图,已知矩形ABCD的边AB=9,AD=4.5,则在边AB上存在( )个点P,使∠DPC=90°
| A.0 | B.1 | C.2 | D.3 |
如图,在平面直角坐标系中,□ABCO的顶点A在 轴上,顶点B的坐标为(4,6).若直线
轴上,顶点B的坐标为(4,6).若直线 将□ABCO分割成面积相等的两部分,则k的值是( )
将□ABCO分割成面积相等的两部分,则k的值是( )
A. |
B. |
C.- |
D.- |
若在△ABC所在平面上求作一点P,使P到∠A的两边的距离相等,且PA=PB,那么下列确定P点的方法正确的是( )
A.P是∠A与∠B两角平分线的交点
B.P为AC、AB两边上的高的交点
C.P为∠A的角平分线与AB的垂直平分线的交点
D.P为∠A的角平分线与AB边上的中线的交点
如图1所示,一只封闭的圆柱形容器内盛了一半水(容器的厚度忽略不计),圆柱形容器底面直径与母线长相等,现将该容器竖起后如图2所示,设图1、图2中水所形成的几何体的表面积分别为S 1、S 2,则S 1与S 2的大小关系是( )
| A.S1≤S 2 | B.S 1<S 2 | C.S 1>S 2 | D.S 1=S 2 |
如果a、b为给定的实数,且1<a<b,设2,a+1, 2a+b,a+b+1这四个数据的平均数为M,这四个数据的中位数为N,则M、N的大小关系是( )
| A.M>N | B.M=N | C.M<N | D.M、N大小不确定 |
如图,为测量被荷花池相隔的两树A,B的距离,数学活动小组设计了如图所示的测量方案:在AB的垂线AP上取两点C,E,再定出AP的垂线FE,使F,C,B在一条直线上.其中三位同学分别测量出了三组数据:①AC,BC ②AC,CE ③EF,CE,AC.能根据所测数据,求得A,B两树距离的是( )
A.② B.①② C.②③ D.①③
边长为2的正六边形,被三组平行线划分成如图所示的小正三角形,从图中任意选定一个正三角形,则选定的正三角形边长恰好是2的概率是( )
A. |
B. |
C. |
D. |
某中学对当天参加课外体育活动的人数和项目进行调查统计,结果绘制成如下两幅不完全统计图.请你根据图中所给信息回答:扇形统计图中“棋类”所占的百分比是 ;本次一共调查了 人.
已知二次函数 (b为常数),当b取不同的值时,对应得到一系列二次函数的图象,它们的顶点都在一条抛物线上,则这条抛物线的解析式是 ;若二次函数
(b为常数),当b取不同的值时,对应得到一系列二次函数的图象,它们的顶点都在一条抛物线上,则这条抛物线的解析式是 ;若二次函数 的顶点只在x轴上方移动,那么b的取值范围是 .
的顶点只在x轴上方移动,那么b的取值范围是 .
已知△ABC中,∠A=α . 在图(1)中∠B、∠C的角平分线交于点O1,则可计算得∠BO1C=90°+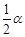 ;在图(2)中,设∠B、∠C的两条三等分角线分别对应交于O1、O2,则∠BO2C= ;请你猜想,当∠B、∠C同时n等分时,(n-1)条等分角线分别对应交于O1、O2,…,On-1, 如图(3),则∠BOn-1C= (用含n和α的代数式表示).
;在图(2)中,设∠B、∠C的两条三等分角线分别对应交于O1、O2,则∠BO2C= ;请你猜想,当∠B、∠C同时n等分时,(n-1)条等分角线分别对应交于O1、O2,…,On-1, 如图(3),则∠BOn-1C= (用含n和α的代数式表示).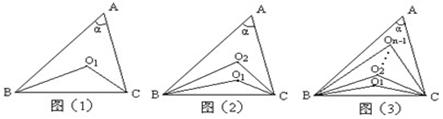
如图,反比例函数 (k≠0)经过点A,连结OA,设OA与x轴的夹角为
(k≠0)经过点A,连结OA,设OA与x轴的夹角为 .
.
(1)求反比例函数解析式;
(2)若点B是反比例函数图象上的另一点,且点B的横坐标为sin ,请你求出sin
,请你求出sin 的值后,写出点B的坐标,并在图中画出点B的大致位置.
的值后,写出点B的坐标,并在图中画出点B的大致位置.
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,对人体健康和大气环境质量的影响更大. 2012年2月,国务院同意发布新修订的《环境空气质量标准》增加了PM2.5监测指标. 我国PM2.5标准采用世卫组织(WHO)设定最宽限值:即日平均浓度小于75微克/立方米为安全值,而WHO标准为日平均浓度值小于25微克/立方米是安全值. 根据某市40个国控监测点某日PM2.5监测数据,绘制成如下所示的频数分布表.
根据表中提供的信息解答下列问题:
(1) 频数分布表中的a= , b= , c= ;
(2) 补充完整答题卡上的频数分布直方图;
(3)在40个国控监测点中,这天的PM2.5日平均浓度值符合我国PM2.5标准安全值的监测点所占比例是 ;
(4) 如果全市共有100个测量点,那么这天的PM2.5日平均浓度值符合WHO标准安全值的监测点约有多少个?
如图,已知∠A,请你仅用尺规,按下列要求作图和计算(不必写画法):
(1)选取适当的边长,在所给的∠A图形上画一个含∠A 的直角三角形ABC,并标上字母,其中点C为直角顶点,点B为另一锐角顶点;
(2)以AC为一边作等边△ACD;
(3)若设∠A=30°、BC边长为a,则BD的长为 .

某商店采购了某品牌的T恤、衬衫、裤子共60件,每款服装按进价至少要购进10件,且恰好用完所带的进货款3700元.设购进T恤x件,衬衫y件.三款服装的进价和预售价如下表:
(1)求出y与x之间的函数关系式;
(2)假设所购进服装全部售出,该商店在采购和销售的过程中需支出各种费用共300元.
①求出预估利润W(元)与T恤x(件)的函数关系式;(注:预估利润W=预售总额-进货款-各种费用)
②求出预估利润的最大值,并写出此时对应购进各款服装多少件.
如图,已知等腰Rt△ABC中,∠ACB=90°,点D为等腰Rt△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
(1)求证:DE平分∠BDC;
(2)连结BE,设DC=a,求BE的长.

如图,已知梯形ABCD的下底边长AB=8cm,上底边长DC=1cm,O为AB的中点,梯形的高DO=4cm. 动点P自A点出发,在AB上匀速运行,动点Q自点B出发,沿B→C→D→A匀速运行,速度均为每秒1个单位,当其中一个动点到达终点时,另一动点也同时停止运动. 设点P运动t(秒)时,△OPQ的面积为S(不能构成△OPQ的动点除外).
(1)求S随t变化的函数关系式及t的取值范围;
(2)当t为何值时S的值最大?说明理由.





 中的a取下列某个值时,该方程有解,则这个a是( )
中的a取下列某个值时,该方程有解,则这个a是( ) ,
, ,那么
,那么 可以表示为( )
可以表示为( )


 ,
, ,-π,-3 这四个数中,最小的数是 ;最大的数是________.
,-π,-3 这四个数中,最小的数是 ;最大的数是________. 是关于x,y二元一次方程
是关于x,y二元一次方程 的解,则(a+1)(a-1)=
的解,则(a+1)(a-1)= :
:
 粤公网安备 44130202000953号
粤公网安备 44130202000953号