已知抛物线y=ax2+bx+c ，当x=0时，有最小值为1 ；且在直线y=2上截得的线段长为4 .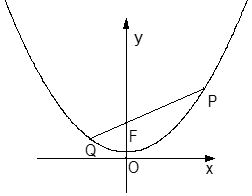
（1）求此抛物线的解析式；
（2）若点P是抛物线的任意一点，记点P到X轴的距离为d1，点P 与点 F （0，2）的距离为d 2 ，猜想d1、 d 2的大小关系，并证明；
（3）若直线PF交此抛物线于另一点Q（异于P点）。 试判断以PQ为直径的圆与x 轴的位置关系，并说明理由。
如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，A、C分别在坐标轴上，点B的坐标为（4，2），直线
交AB，BC分别于点M，N，反比例函数
的图象经过点M，N．
（1）求反比例函数的解析式；
（2）若点P在y轴上，且△OPM的面积与四边形BMON的面积相等，求点P的坐标．
如图，一艘海上巡逻船在A地巡航，这时接到B地海上指挥中心紧急通知：在指挥中心北偏西60°方向的C地，有一艘渔船遇险，要求马上前去救援．此时C地位于北偏西30°方向上，A地位于B地北偏西75°方向上，A、B两地之间的距离为12海里．求A、C两地之间的距离（参考数据：
≈1.41，
≈1.73，
≈2.45，结果精确到0.1）
，其中x满足
．如图，二次函数
的图象与x轴交于点A（﹣3，0）和点B，以AB为边在x轴上方作正方形ABCD，点P是x轴上一动点，连接DP，过点P作DP的垂线与y轴交于点E．
（1）请直接写出点D的坐标： ；
（2）当点P在线段AO（点P不与A、O重合）上运动至何处时，线段OE的长有最大值，求出这个最大值；
（3）是否存在这样的点P，使△PED是等腰三角形？若存在，请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积；若不存在，请说明理由．
增强公民的节约意识，合理利用天然气资源，某市自1月1日起对市区民用管道天然气价格进行调整，实行阶梯式气价，调整后的收费价格如表所示：
| 每月用气量 |
单价（元/m3） |
| 不超出75m3的部分 |
2.5 |
| 超出75m3不超出125m3的部分 |
a |
| 超出125m3的部分 |
a+0.25 |
（1）若甲用户3月份的用气量为60m3，则应缴费 元；
（2）若调价后每月支出的燃气费为y（元），每月的用气量为x（m3），y与x之间的关系如图所示，求a的值及y与x之间的函数关系式；
（3）在（2）的条件下，若乙用户2、3月份共用1气175m3（3月份用气量低于2月份用气量），共缴费455元，乙用户2、3月份的用气量各是多少？
粤公网安备 44130202000953号