下表给出了代数式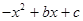 与
与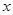 的一些对应值:
的一些对应值:
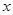 |
…… |
-2 |
-1 |
0 |
1 |
2 |
3 |
…… |
 |
…… |
5 |
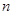 |
c |
2 |
-3 |
-10 |
…… |
(1)根据表格中的数据,确定 ,
, ,
,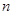 的值;
的值;
(2)设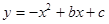 ,直接写出
,直接写出 时
时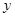 的最大值.
的最大值.
已知函数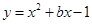 的图象经过点(3,2).
的图象经过点(3,2).
(1)求这个函数的解析式;
(2)当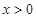 时,求使
时,求使 的x的取值范围.
的x的取值范围.
已知抛物线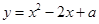 (
(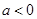 )与
)与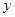 轴相交于点
轴相交于点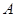 ,顶点为
,顶点为 .直线
.直线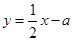 分别与
分别与 轴,
轴,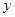 轴相交于
轴相交于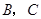 两点,并且与直线
两点,并且与直线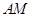 相交于点
相交于点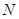 .
.
(1)填空:试用含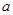 的代数式分别表示点
的代数式分别表示点 与
与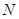 的坐标,则
的坐标,则 ;
;
(2)如图,将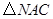 沿
沿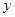 轴翻折,若点
轴翻折,若点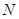 的对应点
的对应点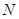 ′恰好落在抛物线上,
′恰好落在抛物线上,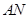 ′与
′与 轴交于点
轴交于点 ,连结
,连结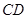 ,求
,求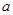 的值和四边形
的值和四边形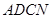 的面积;
的面积;
(3)在抛物线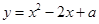 (
(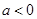 )上是否存在一点
)上是否存在一点 ,使得以
,使得以 为顶点的四边形是平行四边形?若存在,求出
为顶点的四边形是平行四边形?若存在,求出 点的坐标;若不存在,试说明理由.
点的坐标;若不存在,试说明理由.
抛物线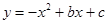 过点(0,-3)和(2,1),试确定抛物线的解析式,并求出抛物线与x轴的交点坐标.
过点(0,-3)和(2,1),试确定抛物线的解析式,并求出抛物线与x轴的交点坐标.
(本题5分)以直线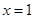 为对称轴的抛物线过点(3,0),(0,3),求此抛物线的解析式.
为对称轴的抛物线过点(3,0),(0,3),求此抛物线的解析式.
如图8所示,有一座抛物线形拱桥,桥下面在正常水位AB时,宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m.以拱桥的最高点为原点建立如图的坐标系,求抛物线的解析式;
若洪水到来时,水位以每小时
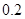 m的速度上升,从警戒线开始,再持续多少小时才能到达拱桥顶.
m的速度上升,从警戒线开始,再持续多少小时才能到达拱桥顶.
已知二次函数的顶点坐标为(3,-1),且其图象经过点(4,1),求此二次函数的解析式.
已知二次函数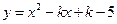 .
.
⑴求证:无论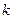 取何实数,此二次函数的图像与
取何实数,此二次函数的图像与 轴都有两个交点;
轴都有两个交点;
⑵若此二次函数图像的对称轴为 ,求它的解析式;
,求它的解析式;