如图3,从地面坚直向上抛出一个小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的关系式为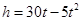 ,那么小球从抛出至回落到地面所需要的时间是:
,那么小球从抛出至回落到地面所需要的时间是:
| A.6s | B.4s | C.3s | D.2s |
二次函数 的图像与
的图像与 图像的形状、开口方向相同,只是位置不同,则二次函数
图像的形状、开口方向相同,只是位置不同,则二次函数 的顶点坐标是
的顶点坐标是
A. |
B. |
C. |
D. |
如图2,从地面竖立向上抛出一个小球,小球的高度h(单位:m)与 小球运动时间t(单位:s)之间的关系式为h=30t-5t2,那么小球从抛出至回落到地面所需要的时间是( ).
| A.6s | B.4s | C.3s | D.2s |
二次函数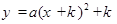 ,当k取不同的实数值时,图像顶点所在的直线是( )
,当k取不同的实数值时,图像顶点所在的直线是( )
A. |
B.x轴 | C.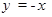 |
D.y轴 |
二次函数y=ax2+bx的图象如图所示,那么一次函数y=ax+b的图象大致是
A. |
B. |
C. |
D. |
用配方法将二次函数y= x²-2x+1写成y=a(x-h)²+k的形式是( )
x²-2x+1写成y=a(x-h)²+k的形式是( )
A.y= (x-2)²-1 (x-2)²-1 |
B.y= (x-1)²-1 (x-1)²-1 |
C.y= (x-2)²-3 (x-2)²-3 |
D.y= (x-1)²-3 (x-1)²-3 |
抛物线y=3x2,y=-3x2,y= x2+3共有的性质是( )
x2+3共有的性质是( )
| A.开口向上 | B.对称轴是y轴 |
| C.都有最高点 | D.y随x值的增大而增大 |
关于抛物线y=(x-1)2-2,下列说法中错误的是
| A.顶点坐标为(1,-2) |
| B.对称轴是直线x=1 |
| C.当x>1时,y随x的增大而减小 |
| D.开口方向向上 |
抛物线y=x2+2x-1关于y轴对称的抛物线的解析式为 ( )
| A.y=x2-2x-1 | B.y=x2-2x-3 |
| C.y=-x2+2x-3 | D.y=-x2-2x-1 |
二次函数y=ax2+bx+c的图象如图所示.现有下列4个判断:①ac<0; ②a+b=0;③4ac-b2=4a;④a+b+c<0,其中正确的有( )

| A.1个 | B.2个 | C.3个 | D.4个 |
下列函数中,不是二次函数的是( )
A.y=1- x2 x2 |
| B.y=2(x-1)2+4 |
C.y= (x-1)(x+4) (x-1)(x+4) |
| D.y=(x-2)2-x2 |
抛物线 上部分点的横坐标x,纵坐标y的对应值如下表:
上部分点的横坐标x,纵坐标y的对应值如下表:
| x |
… |
 |
 |
0 |
1 |
2 |
… |
| y |
… |
0 |
4 |
6 |
6 |
4 |
… |
由上表可知,下列说法正确的个数是 ( )
①抛物线与x轴的一个交点为 ②抛物线与
②抛物线与 轴的交点为
轴的交点为
③抛物线的对称轴是: ④在对称轴左侧y随x增大而增大
④在对称轴左侧y随x增大而增大
A.1 B.2 C.3 D.4
如图所示的抛物线是二次函数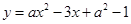 的图像,那么下列结论错误的是……………………………………………………………( )
的图像,那么下列结论错误的是……………………………………………………………( )
A.当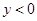 时, 时,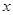 > >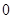 ; ; |
B.当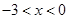 时, 时,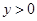 ; ; |
C.当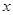 < <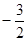 时, 时,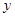 随 随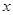 的增大而增大; 的增大而增大; |
D.上述抛物线可由抛物线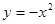 平移得到. 平移得到. |