如图,抛物线y=ax2+c经过点A(0,2)和点B(-1,0).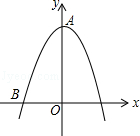
(1)求此抛物线的解析式;
(2)将此抛物线平移,使其顶点坐标为(2,1),平移后的抛物线与x轴的两个交点分别为点C,D(点C在点D的左边),求点C,D的坐标;
(3)将此抛物线平移,设其顶点的纵坐标为m,平移后的抛物线与x轴两个交点之间的距离为n,若1<m<3,直接写出n的取值范围.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
①b2﹣4ac>0;
②4a+c>2b;
③(a+c)2>b2;
④x(ax+b)≤a﹣b.
其中正确结论的是①②④.(请把正确结论的序号都填在横线上)
如图,抛物线y= 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
(1)求点A、B的坐标;
(2)设D为已知抛物线的对称轴上的任意一点,当△ACD的面积等于△ACB的面积时,求点D的坐标;
(3)若直线l过点E(4,0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式.
二次函数y=x2-2mx+3(m> )的图象与x轴交于点A(a,0)和点B(a+n,0)(n>0且n为整数),与y轴交于C点.
)的图象与x轴交于点A(a,0)和点B(a+n,0)(n>0且n为整数),与y轴交于C点.
(1)若a=1,①求二次函数关系式;②求△ABC的面积;
(2)求证:a=m- ;
;
(3)线段AB(包括A、B)上有且只有三个点的横坐标是整数,求a的值.
某企业生产的一批产品上市后30天内全部售完,调查发现,国内市场的日销售量为y1(吨)与时间t(t为整数,单位:天)的关系如图1所示的抛物线的一部分,而国外市场的日销售量y2(吨)与时间t,t为整数,单位:天)的关系如图2所示.
(1)求y1与时间t的函数关系式及自变量t的取值范围,并写出y2与t的函数关系式及自变量t的取值范围;
(2)设国内、国外市场的日销售总量为y吨,直接写出y与时间t的函数关系式,当销售第几天时,国内、外市场的日销售总量最早达到75吨?
(3)判断上市第几天国内、国外市场的日销售总量y最大,并求出此时的最大值.
抛物线与x轴交于A,B两点,(点B在点A的左侧)且A,B两点的坐标分别为(-2,0)、(8,0),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线L交抛物线于点Q,交BD于点M.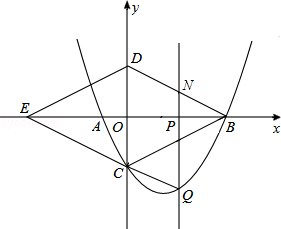
(1)求抛物线的解析式;
(2)当点P在线段OB上运动时,试探究m为何值时,四边形CQMD是平行四边形?
(3)在(2)的结论下,试问抛物线上是否存在点N(不同于点Q),使三角形BCN的面积等于三角形BCQ的面积?若存在,请求出点N的坐标;若不存在,请说明理由.
若抛物线y=x2-2x+c与y轴的交点为(0,-3),则下列说法不正确的是( )
| A.抛物线开口向上 |
| B.抛物线的对称轴是x=1 |
| C.当x=1时,y的最大值为-4 |
| D.抛物线与x轴的交点为(-1,0),(3,0) |
一个小球被抛出后,如果距离地面的高度h(米)和运行时间t(秒)的函数解析式为h=-5t2+10t+1,那么小球到达最高点时距离地面的高度是( )
| A.1米 | B.3米 | C.5米 | D.6米 |
下列四个命题中,正确的是 (填写正确命题的序号)
①三角形的外心是三角形三边垂直平分线的交点;
②函数 与x轴只有一个交点,则
与x轴只有一个交点,则 ;
;
③半径分别为1和2的两圆相切,则两圆的圆心距为3;
④若对于任意x>1的实数,都有ax>1成立,则a的取值范围是a≥1.
抛物线 (a,b,c为常数,且
(a,b,c为常数,且 )经过点(﹣1,0)和(m,0),且1<m<2,当x<﹣1时,y随着x的增大而减小.下列结论:
)经过点(﹣1,0)和(m,0),且1<m<2,当x<﹣1时,y随着x的增大而减小.下列结论:
①abc>0;
②a+b>0;
③若点A(﹣3, ),点B(3,
),点B(3, )都在抛物线上,则
)都在抛物线上,则 <
< ;
;
④ ;
;
⑤若若 ,则
,则 .
.
其中结论错误的是 .(只填写序号)
已知抛物线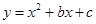 与x轴交于A,B两点,与y轴交于点C,O是坐标原点,点A的坐标是(﹣1,0),点C的坐标是(0,﹣3).
与x轴交于A,B两点,与y轴交于点C,O是坐标原点,点A的坐标是(﹣1,0),点C的坐标是(0,﹣3).
(1)求抛物线的函数表达式;
(2)求直线BC的函数表达式和∠ABC的度数;
(3)P为线段BC上一点,连接AC,AP,若∠ACB=∠PAB,求点P的坐标.
如图是二次函数 (
( )图象的一部分,对称轴是直线x=﹣2.关于下列结论:①ab<0;②
)图象的一部分,对称轴是直线x=﹣2.关于下列结论:①ab<0;② ;③9a﹣3b+c<0;④b﹣4a=0;⑤方程
;③9a﹣3b+c<0;④b﹣4a=0;⑤方程 的两个根为
的两个根为 ,
, ,其中正确的结论有( )
,其中正确的结论有( )
| A.①③④ | B.②④⑤ | C.①②⑤ | D.②③⑤ |
如图,抛物线
与
轴交于
两点,顶点
关于
轴的对称点是
.

(1)求抛物线的解析式;
(2)若直线
与此抛物线的另一个交点为
,求
的面积;
(3)是否存在过
两点的抛物线,其顶点
关于
轴的对称点为
,使得四边形
为正方形?若存在,求出此抛物线的解析式;若不存在,请说明理由.