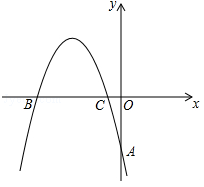
如图,在平面直角坐标系中,抛物线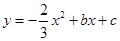 ,经过A(0,﹣4),B(
,经过A(0,﹣4),B(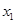 ,0),C(
,0),C(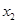 ,0)三点,且
,0)三点,且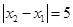 .
.
(1)求b,c的值;
(2)在抛物线上求一点D,使得四边形BDCE是以BC为对角线的菱形;
(3)在抛物线上是否存在一点P,使得四边形BPOH是以OB为对角线的菱形?若存在,求出点P的坐标,并判断这个菱形是否为正方形?若不存在,请说明理由.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则函数y= 与y=bx+c在同一直角坐标系内的大致图象是( )
与y=bx+c在同一直角坐标系内的大致图象是( )
A. |
B. |
C. |
D. |
(满分14分)如图,抛物线经过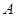 (
(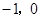 ),
), (
( ),
),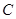 (
(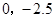 )三点.
)三点.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点 ,使
,使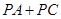 的值最小,求点
的值最小,求点 的坐标;
的坐标;
(3)点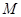 为
为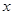 轴上一动点,在抛物线上是否存在点
轴上一动点,在抛物线上是否存在点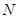 ,使得以
,使得以 四点为顶点的四边形为平行四边形?若存在,请直接写出点
四点为顶点的四边形为平行四边形?若存在,请直接写出点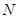 的坐标.
的坐标.
(本题12分)某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球运行时,设乒乓球与端点A的水平距离为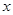 (米),与桌面的高度为
(米),与桌面的高度为 (米),运行时间为
(米),运行时间为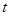 (秒),经多次测试后,得到如下部分数据:
(秒),经多次测试后,得到如下部分数据:
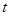 (秒) (秒) |
0 |
0.16 |
0.2 |
0.4 |
0.6 |
0.64 |
0. 8 |
… |
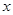 (米) (米) |
0 |
0.4 |
0.5 |
1 |
1.5 |
1.6 |
2 |
… |
 (米) (米) |
0.25 |
0.378 |
0.4 |
0.45 |
0.4 |
0.378 |
0.25 |
… |
(1)当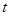 为何值时,乒乓球达到最大高度?
为何值时,乒乓球达到最大高度?
(2)乒乓球落在桌面时,与端点A的水平距离是多少?
(3)乒乓球落在桌面上弹起后, 与
与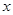 满足
满足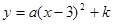
①用含 的代数式表示
的代数式表示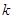 ;
;
②球网高度为0.14米,球桌长(1.4×2)米,若球弹起后,恰好有唯一的击球点,可以将球沿直线扣杀到点A,求 的值.
的值.
如图,抛物线 交
交 轴于点A(
轴于点A( ,0)和B(
,0)和B( , 0),交
, 0),交 轴于点C,抛物线的顶点为D。下列四个命题:
轴于点C,抛物线的顶点为D。下列四个命题:
①当 时,
时, ;
;
②若 ,则
,则 ;
;
③抛物线上有两点P( ,
, )和Q(
)和Q( ,
, ),若
),若 ,且
,且 ,则
,则 ;
;
④点C关于抛物线对称轴的对称点为E,点G,F分别在 轴和
轴和 轴上,当
轴上,当 时,四边形EDFG周长的最小值为
时,四边形EDFG周长的最小值为 。
。
其中真命题的序号是( )
A.① B.② C.③ D.④
如图,在平面直角坐标系中,正方形ABCD和正方形DEFG的边长分别为 ,点A、D、G在
,点A、D、G在 轴上,坐标原点O为AD的中点,抛物线
轴上,坐标原点O为AD的中点,抛物线 过C、F两点,连接FD并延长交抛物线于点M.
过C、F两点,连接FD并延长交抛物线于点M.
(1)若 ,求m和b的值;
,求m和b的值;
(2)求 的值;
的值;
(3)判断以FM为直径的圆与AB所在直线的位置关系,并说明理由.
抛物线y=ax2+bx+4(a≠0)过点A(1,﹣1),B(5,﹣1),与y轴交于点C.
(1)求抛物线的函数表达式;
(2)如图1,连接CB,以CB为边作▱CBPQ,若点P在直线BC上方的抛物线上,Q为坐标平面内的一点,且▱CBPQ的面积为30,求点P的坐标;
(3)如图2,⊙O1过点A、B、C三点,AE为直径,点M为 上的一动点(不与点A,E重合),∠MBN为直角,边BN与ME的延长线交于N,求线段BN长度的最大值.
如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )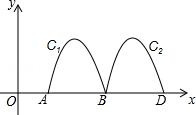
A.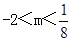 B.
B.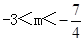
C.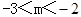 D.
D.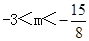
将抛物线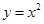 向右平移2个单位,再向上平移3个单位后,抛物线的解析式为( )
向右平移2个单位,再向上平移3个单位后,抛物线的解析式为( )
A. |
B. |
C.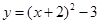 |
D.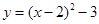 |
一次函数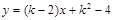 的图象经过原点,则
的图象经过原点,则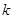 的值为( ).
的值为( ).
| A.2 | B.-2 | C.2或-2 | D.3 |
函数y=x2+2x+1,当y=0时,x=_______________;当1<x<2时,y随x的增大而_____________(填写“增大”或“减小”)