某高级中学为每个学生编号,设定末尾用1表示男生,用2表示女生。如果编号058432表示“2005年入学的8班43号同学,是位女生”,那么今年入学的6班23号男生同学的编号是______________。
火车票上的车次号有两个意义,一是数字越小表示车速越快,1~98次为特快列车,101~198次为直快列车,301~398次为普快列车,401~498次为普客列车;二是单数与双数表示不同的行驶方向,其中单数表示从北京开出,双数表示开往北京。根据以上规定,杭州开往北京的某一直快列车的车次号可能是 ( )
| A.20 | B.119 | C.138 | D.319 |
观察下面的图形,它们是按一定规律排列的,依照此规律,第_ 个图形中有190 个五角星。
如图,连接在一起的两个正方形的边长都为1cm,一个微型机器人由点A开始按ABCDEFCGA…的顺序沿正方形的边循环移动.①第一次到达点G时,微型机器人移动了 cm;②当微型机器人移动了2012cm时,它停在 点.
下图是在正方形网格中按规律填成的阴影,根据此规律,则第n个图中阴影部
分小正方形的个数是 .
如下表,从左到右在每个小格子中都填入一个整数,使得其中任意三个相邻格子中 所填整数之和都相等,则第2012个格子中的数为( )
| 3 |
a |
b |
c |
﹣1 |
|
|
|
2 |
|
… |
A.3 B.2 C.0 D.﹣1
如图是由正三角形、正方形及正六边形组成的图案,按此规律,第16个图案中,正三角形的个数为( )
| A.82 | B.72 | C.83 | D.73 |
在ΔABC中,D为BC的中点,E为AC上的任意一点,BE交AD于点O.某学生在研究这一问题时,发现了如下事实: 如图1,当 时,有
时,有 ;
;
如图2,当 时,有
时,有 ;
;
如图3,当 时,有
时,有 ;在图4中,当
;在图4中,当 时,
时,
参照上述研究的结论,请你猜想用n表示AO∶AD的一般结论,并给出证明.



一种电讯信号转发装置的发射直径为31km.现要求:在一边长为30km的正方形城区选择若干个安装点,每个点安装一个这种转发装置,使这些装置转发的信号能完全覆盖这个城市.问:
(1)能否找到这样的4个安装点,使得这些点安装了这种转发装置后能达到预设的要求?
(2)至少需要选择多少个安装点,才能使这些点安装了这种转发装置后达到预设的要求?
答题要求:请你在解答时,画出必要的示意图,并用必要的计算、推理和文字来说明你的理由.(下面给出了几个边长为30km的正方形城区示意图,供解题时选用)
图1 图2 图3 图4
某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1.在温室内,沿前侧内墙保留3m宽的空地,其它三侧内墙各保留1m宽的通道.当矩形温室的长与宽各为多少时,蔬菜种植区域的面积是288m2?
我国从2008年6月1日起执行“限塑令”.“限塑令”执行前,某校为了了解本校学生所在家庭使用塑料袋的数量情况,随机调查了10名学生所在家庭月使用塑料袋的数量,结果如下(单位:只):
65,70,85,75,85,79,74,91,81,95.
(1)计算这10名学生所在家庭平均月使用塑料袋多少只?
(2)“限塑令”执行后,家庭月使用塑料袋数量预计将减少50%.根据上面的计算结果,估计该校1 000名学生所在家庭月使用塑料袋可减少多少只?
我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段 的最小覆盖圆就是以线段
的最小覆盖圆就是以线段 为直径的圆.
为直径的圆.
(1)请分别作出图1中两个三角形的最小覆盖圆(要求用尺规作图,保留作图痕迹,不写作法);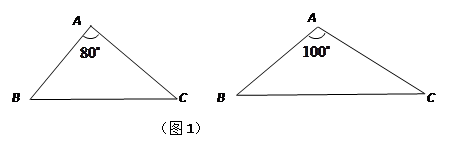
(2)探究三角形的最小覆盖圆有何规律?请写出你所得到的结论(不要求证明);
(3)某地有四个村庄 (其位置如图2所示),现拟建一个电视信号中转站,为了使这四个村庄的居民都能接收到电视信号,且使中转站所需发射功率最小(距离越小,所需功率越小),此中转站应建在何处?请说明理由.
(其位置如图2所示),现拟建一个电视信号中转站,为了使这四个村庄的居民都能接收到电视信号,且使中转站所需发射功率最小(距离越小,所需功率越小),此中转站应建在何处?请说明理由.