已知梯形 中,
中, ∥
∥ ,
, ,
, ,
, ,
, .动点
.动点 从
从 点开始以
点开始以 的速度沿线段
的速度沿线段 向
向 点运动,动点
点运动,动点 从点
从点 开始以
开始以 的速度沿线段
的速度沿线段 向
向 点运动.点
点运动.点 、点
、点 分别从
分别从 、
、 两点同时出发,当其中一点停止时,另一点也随之停止。设运动时间为
两点同时出发,当其中一点停止时,另一点也随之停止。设运动时间为 .
.
(1)求 的长;
的长;
(2)以 为圆心、
为圆心、 长为半径的
长为半径的 与直线
与直线 相切时,求
相切时,求 的值;
的值;
(3)是否存在 的值,使得以
的值,使得以 为圆心、
为圆心、 长为半径的
长为半径的 与以
与以 为圆心、
为圆心、 长为半径的
长为半径的 相切?若存在,求出
相切?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
璧山观音塘湿地公园是目前重庆最大的湿地公园,该公园以众多珍稀动植物和独特的灯光和喷泉,吸引着越来越多的游客前往游玩。为了应对游客在游玩过程中的意外伤害,公园决定在形状为如图所示的四边形中央广场内修建一个便民取药点 ,以便在里面配置各种应急药物。现要求该取药点离两个广场入口
,以便在里面配置各种应急药物。现要求该取药点离两个广场入口 、
、 的距离相等,且离观赏点
的距离相等,且离观赏点 的距离恰好等于
的距离恰好等于 、
、 间的距离。请在原图上利用尺规作图作出取药点
间的距离。请在原图上利用尺规作图作出取药点 的位置。(要求:不写已知、求作、作法和结论,保留作图痕迹,必须用铅笔作图)
的位置。(要求:不写已知、求作、作法和结论,保留作图痕迹,必须用铅笔作图)
课题研究小组对附着在物体表面的三个微生物(课题小组成员把他们分别标号为1,2,3)的生长情况进行观察记录.这三个微生物第一天各自一分为二,产生新的微生物(分别被标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录).那么标号为100的微生物会出现在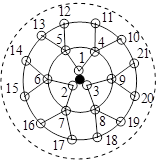
| A.第3天. | B.第4天. | C.第5天. | D.第6天. |
某村有一口水井,水面比井口低3米,一只蜗牛从水面沿着井壁竖直向井口爬,第一次向上爬了0.5米后又向下滑了0.1米;第二次向上爬了0.42米后却又向下滑了0.15米;第三次向上爬了0.7米后却又向下滑了0.15米;第四次向上爬了0.75米后却又向下滑了0.1米;第五次向上爬了0.55米后没有下滑;第六次向上爬了0.48米,问蜗牛有没有爬出井口?
如果我们用“♀”、“♂”来定义新运算:对于任意实数a,b,都有a♀b= a,a♂b= b,例如3♀2=3,3♂2=2。则(人♀民)♀(中♂学)=___________________。
为了让居民有更多休闲和娱乐的地方,政府又新建了几处广场,工人师傅在铺设地面时,准备选用同一种正多边形地砖.现有下面几种形状的正多边形地砖,其中不能进行平面镶嵌的是 ( )
| A.正三角形 | B.正方形 | C.正五边形 | D.正六边形 |
古希腊数学家把数1,3,6,10,15,21,…,叫做三角形数,它有一定的规律性,则第24个三角形数与第22个三角形数的差为 。
某商场进了一种T恤衫30件和一种衬衫20件,T恤衫的售价是m元/件,衬衫的售价是T恤衫的2倍,销售一段时间后,T恤衫和衬衫卖出的数量恰好相同.此时商场决定调价,把T恤衫的售价提高75%,把衬衫的售价降低50%,当商场卖完这两种衣服后,发现这批衬衫和T恤衫的平均售价是一样的,那么调价前卖出的衬衫和T恤衫的数量都是____ __件.
一手机经销商计划购进某品牌的A型、B型、C型三款手机共60部,每款手机至少要购进8部,且恰好用完购机款61000元.设购进A型
手机x部,B型手机y部.三款手机的进价和预售价如下表:
| 手机型号 |
A型 |
B型 |
C型 |
| 进 价(单位:元/部) |
900 |
1200 |
1100 |
| 预售价(单位:元/部) |
1200 |
1600 |
1300 |
(1)用含x,y的式子表示购进C型手机的部数;
(2)求出y与x之间的函数关系式;
(3)假设所购进手机全部售出,综合考虑各种因素,该手机经销商在购销这批手机过程中需另外支出各种费用共1500元.
①求出预估利润P(元)与x(部)的函数关系式;
(注:预估利润P=预售总额-购机款-各种费用)
②求出预估利润的最大值,并写出此时购进三款手机各多少部.
用若干张大小相同的黑白两种颜色的正方形纸片,按下列拼图的规律拼成一列图案,则第6个图案中黑色正方形纸片的张数是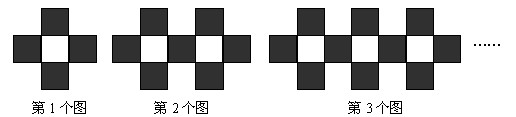
| A.22 | B.21 | C.20 | D.19 |
每个命题都由____________和____________两部分组成.