关于x的不等式组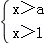 的解集为x>1,则a的取值范围是( )
的解集为x>1,则a的取值范围是( )
| A.a≥1 | B.a>1 | C.a≤1 | D.a<1 |
A,B,C,D四支足球队分在同一小组进行单循环足球比赛,争夺出线权.比赛规则规定:胜一场得3分,平一场得1分,负一场得0分,小组中积分最高的两个队(有且只有两个队)出线.小组赛结束后,如果A队没有全胜,那么A队的积分至少要( )分才能保证一定出线.【注:单循环比赛就是小组内的每一个队都要和其他队赛一场】
| A.7 | B.6 | C.4 | D.3 |
某学校准备购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买2个足球和3个篮球共需340元,购买5个足球和2个篮球共需410元.
(1)购买一个足球、一个篮球各需多少元?
(2)根据学校的实际情况,需购买足球和篮球共96个,并且总费用不超过5720元.问最多可以购买多少个篮球?
若不等式组 的解集中的任何一个x的值均不在2≤x≤5范围内,则a的取值范围是( )
的解集中的任何一个x的值均不在2≤x≤5范围内,则a的取值范围是( )
| A.a<1 | B.a<1或a>5 | C.a≤1或a≥5 | D.a<1且a>5 |
已知关于x的方程4x+2m+1=2x+5的解是负数.
(1)求m的取值范围;
(2)在(1)的条件下,解关于x的不等式2(x﹣2)>mx+3.
解不等式2(x+1)﹣1≥4x+3,并把它的解集在数轴上表示出来.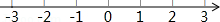
小武新家装修,在装修客厅时,购进彩色地砖和单色地砖共100块,共花费5600元.已知彩色地砖的单价是80元/块,单色地砖的单价是40元/块.
(1)两种型号的地砖各采购了多少块?
(2)如果厨房也要铺设这两种型号的地砖共60块,且采购地砖的费用不超过3200元,那么彩色地砖最多能采购多少块?
若 成立,则下列不等式成立的是( )
成立,则下列不等式成立的是( )
A. |
B. |
C. |
D. |