某商店5月1日举行促销优惠活动,当天到该商店购买商品有两种方案,方案一:用168元购买会员卡成为会员后,凭会员卡购买商店内任何商品,一律按商品价格的8折优惠;方案二:若不购买会员卡,则购买商店内任何商品,一律按商品价格的9.5折优惠.已知王老师5月1日前不是该商店的会员.
(1)若王老师不购买会员卡,所购买商品的价格为120元时,实际应支付多少元?
(2)请帮王老师算一算,所购买商品的价格在什么范围内时,采用方案一更合算?
定义:对于任何数a,符号[a]表示不大于a的最大整数.例如:[5.7]=5,[5]=5,[-1.5]=-2.
(1)[-π]= ;
(2)如果[a]=2,那么a的取值范围是 ;
(3)如果[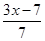 ]=-5,求满足条件的所有整数x;
]=-5,求满足条件的所有整数x;
(4)直接写出方程6x-3[x]+7=0的解.
商店为了对某种商品促销,将定价为3元的商品,以下列方式优惠销售:若购买不超过5件,按原价付款;若一次性购买5件以上,超过部分打八折,现有27元钱,最多可以购买该商品多少件?
已知A、B、C三地是同一条河流上的三个不同地方,且A、B、C在同一直线上,A、C相距28千米,某船先从A地顺流而下来到B地,再立刻调头逆流而上到达C地,一共用了5小时,调头时间忽略不计.已知该船的静水速度为18km/h,水流速度为2km/h,请问:
(1)船在顺水中航行的速度是 km/h,船在逆水中航行的速度是 km/h.
(2)A、B两地相距多少千米?
某玩具厂计划用10天时间加工A、B两种类型的玩具共3600个,该厂每天能加工A型玩具450个或B型玩具300个,由于条件所限,每天只能加工一种类型的玩具,请问该厂应该安排几天加工A型玩具,才能如期完成任务?
已知关于x的方程2x=x+m﹣3和关于y的方程3y﹣2(n﹣1)2=m,试思考:
(1)请用含m的代数式表示方程2x=x+m﹣3的解;
(2)若n=2,且上述两个方程的解互为相反数时,求m的值;
(3)若m=6,n=2时,设方程2x=x+m﹣3的解为x=a,方程3y﹣2(n﹣1)2=m的解为y=b,请比较3b﹣a与2的大小关系,并说明理由.
定义一种新运算“⊕”:a⊕b=a-2b,比如:2⊕(-3)=2-2×(-3)=2+6=8.
(1)求(-3)⊕2的值;
(2)若(x-3)⊕(x+1)=1,求x的值.
定义新运算:对于任意有理数a,b,都有a※b=a(a﹣b)+1,等式右边是通常的加法,减法及乘法运算,比如:2※5=2×(2﹣5)+1=2×(﹣3)+1=﹣6+1=﹣5.
(1)求(﹣2)※3的值;
(2)若3※x=5※(x﹣1),求x的值.
下面是解分式方程的过程,阅读完后请填空:
解方程: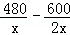 =45.
=45.
解:方程两边都乘以2x,得960﹣600=90x,
解这个方程,得x=4.
经检验,x=4是原方程的根.
第一步计算中的2x是: ;这个步骤用到的依据是 ;
解分式方程与解一元一次方程之间的联系是: .
山地自行车越来越受到中学生的喜爱,各种品牌相继投放市场,某车行经营的A型车去年销售总额为5万元,今年每辆销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
(1)今年A型车每辆售价多少元?
(2)该车行计划新进一批A型车和新款B型车共60辆,要使这批车获利不少于33000元,A型车至多进多少辆?A,B两种型号车的进货和销售价格如表:
| |
A型车 |
B型车 |
| 进货价格(元) |
1100 |
1400 |
| 销售价格(元) |
今年的销售价格 |
2000 |
某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)加工成如图所示的竖式与横式两种无盖的长方形纸箱.(加工时接缝材料不计)
(1)该工厂原计划用若干天加工纸箱200个,后来由于对方急需要货,实际加工时每天加工速度时原计划的1.5倍,这样提前2天超额完成了任务,且总共比原计划多加工40个,问原计划每天加工纸箱多少个;
(2)若该厂购进正方形纸板1000张,长方形纸板2000张.问竖式纸盒,横式纸盒各加工多少个,恰好能将购进的纸板全部用完;
(3)该工厂某一天使用的材料清单上显示,这天一共使用正方形纸板50张,长方形纸板a张,全部加工成上述两种纸盒,且120<a<136,试求在这一天加工两种纸盒时,a的所有可能值.
A,B两地相距160km,一艘船从A出发,顺水航行8h到B,而从B出发逆水航行10h到A,已知船顺水航行、逆水航行的速度分别是静水速度与水流速度的和与差,求船在静水中的速度和水流速度.
据电力部门统计,每天8:00至21:00是用电高峰期,简称“峰时”,21:00至次日8:00是用电低谷期,简称“谷时”.为了缓解供电需求紧张的矛盾,该市电力部门于本月初统一换装“峰谷分时”电表,对用电实行“峰谷分时电价”新政策,具体见下表:
| 时间 |
换表前 |
换表后 |
|
| 峰时(8:00-21:00) |
谷时(21:00-8:00) |
||
| 电价 |
每度0.52元 |
每度0.55元 |
每度0.30元 |
(1)小张家上月“峰时”用电50度,“谷时”用电20度,若上月初换表,则相对于换表前小张家的电费是节省还是浪费?你帮他算一算吧;
(2)小张家这个月用电95度,经测算比换表前使用95度电节约了5.9元,问小张家使用“峰时”电和“谷时”电分别是多少度?