同学们,我们在本期教材的第一章《有理数》中曾经学习过绝对值的概念:一般的,数轴上表示数 的点与原点的距离叫做数
的点与原点的距离叫做数 的绝对值,记作
的绝对值,记作 。
。
实际上,数轴上表示数 的点与原点的距离科技做
的点与原点的距离科技做 :数轴上表示数
:数轴上表示数 的点与表示数
的点与表示数 的点的距离可记作
的点的距离可记作 ,那么,
,那么,(I) ①数轴上表示数
 的点与表示数1的点的距离可记作________
的点与表示数1的点的距离可记作________
②数轴上表示数 的点与表示数2的点的距离可记作________
的点与表示数2的点的距离可记作________
③数轴上表示数 的点与表示数-3的点的距离可记作________
的点与表示数-3的点的距离可记作________(II)数轴上表示到数-2的点的距离为5的点有几个?并求出它们表示的数。
(III)根据(I)中②、③两小题你所填写的结论,请同学们利用数轴探究这两段距离之和的最小值,并简述你的思考过程。
某城市一周的气温统计如下表:
| |
周一 |
周二 |
周三 |
周四 |
周五 |
周六 |
周日 |
| 最高气温 |
9℃ |
10℃ |
7℃ |
6℃ |
7℃ |
9℃ |
8℃ |
| 最低气温 |
0℃ |
2℃ |
-4℃ |
-3℃ |
-1℃ |
-1℃ |
0℃ |
(I)分别计算该城市这一周中最高气温和最低气温的平均值;
(II)在这一周七天当中,周几的温差(最高气温-最低气温)最大?最大值是多少?
画出数轴,在数轴表示下列个数,然后用“<”把这些数连接起来。
已知点 在数轴上分别表示
在数轴上分别表示 。
。⑴填写下表:
| m |
5 |
-5 |
-6 |
-6 |
-10 |
| n |
3 |
0 |
4 |
-4 |
2 |
| A、B两点的距离 |
|
|
|
|
|
⑵若
 两点的距离为d,则
两点的距离为d,则 与
与 有何数量关系?
有何数量关系?⑶在数轴上是否存在整数点
 ,使它到
,使它到 和
和 的距离之和为
的距离之和为 ?若存在,请写出所有符合条件的整数;若不存在,请说明理由。
?若存在,请写出所有符合条件的整数;若不存在,请说明理由。
观察下面三行数:
—2, 4, —8, 16, —32, 64,… ①
6, —6, 18, —30, 66,… ②
, —1, 2, —4, 8, —16, 32,… ③(1)第①行数按什么规律排列?
(2)第② ③行数与第①行数分别有什么关系?
(3)取每行的第十个数,计算这三个数的和。25. 出租车司机小李某天下午的营运全是在东西走向的人民大街上进行的,如果规定向东为正,向西为负,他这天下午行车里程(单位:千米)如下:
+15,-2,+5,-1,+10,-3,-2,+12,+4,-5,+6
(1)小李下午出发地记为0,他将最后一名乘客送抵目的地时,小李距下午出车时的出发地有多远?(2)若汽车耗油量为0.41升/千米,这天下午小李共耗油多少升?
(本题6分)某人去水果批发市场采购苹果,他看中了A、B两家苹果。这两家苹果品质一样,零售价都为6元/千克,批发价各不相同。
A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠。
B家的规定如下表:
| 数量范围(千克) |
0~500 |
500以上~1500 |
1500以上~2500 |
2500以上 |
| 价 格(元) |
零售价的95% |
零售价的85% |
零售价的75% |
零售价的70% |
【表格说明:批发价格分段计算,如:某人批发苹果2100千克,则总费用=6×95%×500+6×85%×1000+6×75%×(2100-1500)】(1)如果他批发600千克苹果,则他在A 家批发需要 元,在B家批发需要 元;
(2) 如果他批发x千克苹果(1500<x<2000),则他在A 家批发需要 元,在B家批发需要 元(用含x的代数式表示);
(3) 现在他要批发1800千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由。
(共8分)对于有理数 、
、 ,定义运算:“
,定义运算:“ ”,
”,
(1)计算:3
 (-5)的值;
(-5)的值;(2)填空:
 (填“>”或“=”或“<”);我们知道:有理数的加法运算和乘法运算满足交换律.那么,由以上计算的结果进行猜想:“
(填“>”或“=”或“<”);我们知道:有理数的加法运算和乘法运算满足交换律.那么,由以上计算的结果进行猜想:“ ” 交换律。(填“满足”或“不满足”)
” 交换律。(填“满足”或“不满足”)(3)如果(x-2)
 3=3,求x的值。
3=3,求x的值。
(共10分)有理数 、
、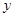 在数轴上对应点如图所示:
在数轴上对应点如图所示: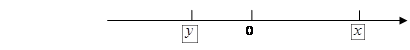
(1)在数轴上表示
 、|y|;
、|y|;(2)试把
 、
、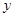 、0、
、0、 、︱y︱这五个数从小到大用“<”号连接起来.
、︱y︱这五个数从小到大用“<”号连接起来.(3)化简|x+y|-|y-x|﹢|y|
应用题。1、某厂一车间上半年生产零件48万件,是下半年产量的
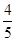 ,该车间全年的产量是多少?
,该车间全年的产量是多少?2、高铁列车的运行速度是380千米/小时,普通列车的速度是它的
 。普通列车的速度是多少?
。普通列车的速度是多少?3、用120cm的铁丝做一个长方体框架。长、宽、高的比是3:2:1。这个长方体的体积是多少?
4、一个圆形花坛。周长是25.12m。如果在这个花坛的周围铺上一条宽1m的环形小路,这条小路的面积是多少平方米?
5、校园里有杨树40棵,是柳树的
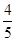 。松树棵数是柳树的
。松树棵数是柳树的 。松树有多少棵?
。松树有多少棵?6、某厂为青海玉树灾区赶制一批帐篷。第一天生产了这批帐篷的
 ,第二天生产了总数的
,第二天生产了总数的 。两天共生产4400顶。第一天生产了多少顶?
。两天共生产4400顶。第一天生产了多少顶?
(本题4分)某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
| 与标准质量的差值(单位:克) |
-5 |
-2 |
0 |
1 |
3 |
6 |
| 袋 数 |
1 |
4 |
3 |
4 |
5 |
3 |
这批样品的平均质量比标准质量多还是少?若每袋标准质量为450克,则抽样检测的总质量是多少?