初中数学有理数无理数的概念与运算试题

下列说法中正确的是 （   ）                                              

A．整数又叫自然数	B．0是整数
C．一个数不是正数就是负数	D．0不是自然数

2012年伦敦奥运会上，中国选手吕小军在男子举重77公斤级比赛中，打破了原奥运会纪录，创造了新抓举纪录，成绩是175公斤，下列说法正确的是（  ）

A．原来奥运会纪录是175公斤	B．原来奥运会纪录是77公斤
C．原来奥运会纪录小于77公斤	D．原来奥运会纪录小于175公斤

七年级一班某次数学测验的平均成绩为80分，数学老师以平均成绩为基准，记作0，把小龙、小聪、小梅、小莉、小刚这五位同学的成绩简记为+10，–15，0，+20，–2．问这五位同学的实际成绩分别是多少分？

=_________  

把下面的直线补充成一条数轴，然后在数轴上标出下列各数：
–3，+l，，－l.5，6.

（1）如图，圆上有五个点，这五个点将圆分成五等份（每一份称为一段弧长），把这五个点按顺时针方向依次编号为1，2，3，4，5，若从某一点开始，沿圆周顺时针方向行走，点的编号是数字几，就走几段弧长，则称这种走法为一次“移位”．如：小明在编号为3的点，那么他应走3段弧长，即从3→4→5→1为第一次“移位”，这时他到达编号为1的点，然后从1→2为第二次“移位”．小明从编号为4的点开始，第三次“移位”后，他到达编号为    的点，第2012次“移位”后，他到达编号为     的点．

（2）若将圆进行二十等份，按照顺时针方向依次编号为1，2，3，…，20，小明从编号为3的点开始，沿顺时针方向，按上述“移位”方式行走，
①经过4次“移位”后，他到达编号为        的点．
②“移位”次数a=      时，小王刚好到达编号为16的点，又满足|a-2012|的值最小．

绝对值大于1而小于4的整数有____________，其和为_________。

由一些正整数组成的数表如下（表中下一行中数的个数是上一行中数的个数的2倍）：

第1行	2
第2行	4   6
第3行	8  10  12  14
…	…

若规定坐标号（）表示第行从左向右第个数，则（4，3）所表示的数是_________；（5，6）与（6，5）表示的两数之积是_________,数1028对应的坐标号是_________ .

已知123456789101112…997998999是由连续整数1至999排列组成的一个数，在该数中从左往右数第2013位上的数字为　   　．

下列结论正确的有（   ）
①符号相反的数互为相反数；
②绝对值等于本身的数有0、1；
③平方后等于本身的数只有0、1；
④若有理数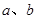互为相反数，则它们一定异号；
⑤立方后等于本身的数是0和1；
⑥倒数等于本身的数是-1和1．

A．2个

B．3个

C．4个

D．5个

下列说法正确的是（ ）
①最大的负整数是-1；  
②数轴上表示数2和-2的点到原点的距离相等；
③当a≤0时，|a|=-a成立；
④a+5一定比a大；
⑤（-2）³和-2³相等．

A．2个

B．3个

C．4个

D．5个

如下图所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第9个图形需要黑色棋子的个数是

A．99

B．80

C．63

D．132

先化简，再求值：，其中．

利用整式乘法公式计算：2014×2012-2013²=_________．

 是一个三位的自然数，已知，这个三位数是218；聪明的小亮在解决这种问题时，采取列成连减竖式的方法（见右图）确定要求的自然数，请你仿照小亮的作法，解决这种问题.如果是一个四位的自然数，且 ，那么，这个四位数是_____________．