初中数学有理数无理数的概念与运算试题

同学们，我们曾经研究过n×n的正方形网格，得到了网格中正方形的总数的表达式为1²+2²+3²+…+n²．但n为100时，应如何计算正方形的具体个数呢?下面我们就一起来探究并解决这个问题．首先，通过探究我们已经知道0×1+1×2+2×3+…+(n—1)×n=n(n+1)(n—1)时，我们可以这样做：
(1)观察并猜想：
1²+2²=(1+0)×1+(1+1)×2=1+0×1+2+1×2=(1+2)+(0×1+1×2)
1²+2²+3²=(1+0)×1+(1+1)×2+(1+2)×3
=1+0×1+2+1×2+3+2×3
=(1+2+3)+(0×1+1×2+2×3)
1²+2²+3²+4²=(1+0)×1+(1+1)×2+(1+2)×3+               
=1+0×1+2+1×2+3+2×3+                        
=(1+2+3+4)+(                                  )
……
(2)归纳结论：
1²+2²+3²+…+n²=(1+0)×1+(1+1)×2+(1+2)×3+…+n
=1+0×1+2+1×2+3+2×3+…+n+(n一1)×n
=(                      ) +
=                      +                                 
=×                     
(3)实践应用：
通过以上探究过程，我们就可以算出当n为100时，正方形网格中正方形的总个数是              ．

我国以2010年11月1日零时为标准计时点，进行了第六次全国人口普查，查得全国总人口约为1370000000人，请将总人口用科学记数法表示为（　　）

A．1.37×10^8	B．1.37×10^9
C．1.37×10^10	D．13.7×10^8

计算﹣3²的值是

A．9

B．－9

C．6

D．－6

|﹣2|的绝对值=　　．

一个纸环链，纸环按红黄绿蓝紫的顺序重复排列，截去其中的一部分，剩下部分如图所示，则被截去部分纸环的个数可能是（　 　）

A．2011

B．2011

C．2012

D．2013

计算
（1）
（2）（a+1）²﹣a（a﹣1）

若是一个正数，那么下列说法正确的是 （ ）                                 

A．a一定是正数

B．a一定是负数

C．a一定不是0

D．a是任何有理数

下列结论正确的有（   ）
①符号相反的数互为相反数；
②绝对值等于本身的数有0、1；
③平方后等于本身的数只有0、1；
④若有理数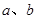互为相反数，则它们一定异号；
⑤立方后等于本身的数是0和1；
⑥倒数等于本身的数是-1和1．

A．2个

B．3个

C．4个

D．5个

下列说法正确的是（ ）
①最大的负整数是-1；  
②数轴上表示数2和-2的点到原点的距离相等；
③当a≤0时，|a|=-a成立；
④a+5一定比a大；
⑤（-2）³和-2³相等．

A．2个

B．3个

C．4个

D．5个

如下图所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第9个图形需要黑色棋子的个数是

A．99

B．80

C．63

D．132

先化简，再求值：，其中．

利用整式乘法公式计算：2014×2012-2013²=_________．

 是一个三位的自然数，已知，这个三位数是218；聪明的小亮在解决这种问题时，采取列成连减竖式的方法（见右图）确定要求的自然数，请你仿照小亮的作法，解决这种问题.如果是一个四位的自然数，且 ，那么，这个四位数是_____________．

计算：．

如果ab<0，那么下列判断正确的是（　　）．

A．a<0，b<0	B．a>0，b>0
C． a≥0，b≤0	D．a<0，b>0或a>0，b<0