小新抛一枚质地均匀的硬币，连续抛三次，硬币落地均正面朝上，如果他第四次抛硬币，那么硬币正面朝上的概率为（ ）
A． |
B． |
C．1 | D． |
下列说法正确的是（ ）
①试验条件不会影响某事件出现的频率；
②在相同的条件下试验次数越多，就越有可能得到较精确的估计值，但各人所得的值不一定相同；
③如果一枚骰子的质量分布均匀，那么抛掷后每个点数出现的机会均等；
④抛掷两枚质量分布均匀的相同的硬币，出现“两个正面”、“两个反面”、“一正一反”的机会相同．
| A．①② | B．②③ | C．③④ | D．①③ |
在对某次实验数据整理过程中，某个事件出现的频率随实验次数变化析线图如图所示，则符合这一结果的实验最有可能的是（ ）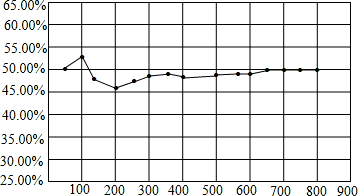
| A．抛一个质地均匀的正六面体骰子，向上的面点数是4 |
| B．暗箱中有1个红球和2个黄球，它们只有颜色上的区别，从中任取一球是黄球 |
| C．一副的普通扑克牌洗匀后，从中任取一张牌的花色是红桃 |
| D．抛硬币实验中关注正面出现的概率 |
小明任意掷一枚均匀的骰子5次，数字3正面朝上共出现了4次，则小明任意抛掷该骰子一次，数字3正面朝上的概率是（ ）
A． |
B． |
C． |
D．不能确定 |
一只蚂蚁在如图所示的正方形地砖上爬行，蚂蚁停留在阴影部分的概率为（ ）
A． |
B． |
C． |
D． |
某小组做“用频率估计概率”的实验时，统计了某一结果出现的频率，绘制了如图的折线统计图，则符合这一结果的实验最有可能的是（ ）
| A．在“石头、剪刀、布”的游戏中，小明随机出的是“剪刀” |
| B．一副去掉大小王的普通扑克牌洗匀后，从中任抽一张牌的花色是红桃 |
| C．暗箱中有1个红球和2个黄球，它们只有颜色上的区别，从中任取一球是黄球 |
| D．掷一个质地均匀的正六面体骰子，向上的面点数是4 |
如图，在方格纸中，随机选择标有序号①②③④⑤中的一个小正方形涂黑，与图中阴影部分构成轴对称图形的概率是（ ）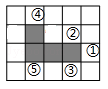
A． |
B． |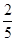
C． |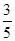
D． |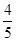
在6张完全相同的卡片上分别画上线段、等边三角形、平行四边形、圆、正方形、直角梯形，在看不见图形的情况下随机摸出1张，这张卡片上的图形既是中心对称图形又是轴对称图形的概率是（ ）
A． |
B． |
C． |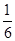
D． |
“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形（如图所示）．小亮同学随机地在大正方形及其内部区域投针，若直角三角形的两条直角边的长分别是2和1，则针扎到小正方形（阴影）区域的概率是（ ）
A． |
B． |
C． |
D． |
小明和同学做“抛掷质地均匀的硬币试验”获得的数据如表：
抛掷次数 |
100 |
200 |
300 |
400 |
500 |
正面朝上的频数 |
53 |
98 |
156 |
202 |
244 |
若抛掷硬币的次数为1000，则“正面朝上”的频数最接近
A．20B．300C．500D．800
某小组做“用频率估计概率”的试验时，绘出的某一结果出现的频率折线图，则符合这一结果的试验可能是
A．抛一枚硬币，出现正面朝上
B．掷一个正六面体的骰子，出现3点朝上
C．一副去掉大小王的扑克牌洗匀后，从中任抽一张牌的花色是红桃
D．从一个装有2个红球1个黑球的袋子中任取一球，取到的是黑球
某射击运动员在同一条件下的射击成绩记录如下：
| 射击次数 |
20 |
80 |
100 |
200 |
400 |
1000 |
| "射中九环以上"的次数 |
18 |
68 |
82 |
168 |
327 |
823 |
| "射中九环以上"的频率（结果保留两位小数） |
0.90 |
0.85 |
0.82 |
0.84 |
0.82 |
0.82 |
根据频率的稳定性，估计这名运动员射击一次时"射中九环以上"的概率约是
| A． |
0.90 |
B． |
0.82 |
C． |
0.85 |
D． |
0.84 |
一个布袋里有6只颜色不同的球，其中2个红球，4个白球，从布袋里任意摸出一个球，则摸出的球的红球的概率为（ ）
A． |
B． |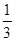
C． |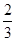
D． |
同时投掷两个骰子，点数和为5的概率是（ ）
A． |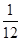
B． |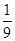
C． |
D． |
在
□4a□4空格□中，任意填上“+”或“-”，在所得到的所有代数式中，能构成完全平方式的概率是（ ）
| A．1 | B． |
C． |
D． |
粤公网安备 44130202000953号