从一个不透明的口袋中随机摸出一球,再放回袋中,不断重复上述过程,一共摸了150次,其中有50次摸到黑球,已知囗袋中仅有黑球10个和白球若干个,这些球除颜色外,其他都一样,由此估计口袋中有 个白球.
一个口袋中有红球、白球共10个,这些球除颜色外都相同,将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了100次球,发现有71次摸到红球.请你估计这个口袋中红球的数量为 个.
在不透明的口袋中有若干个完全一样的红色小球,现放入10个仅颜色不同的白色小球,均匀混合后,有放回的随机摸取30次,有10次摸到白色小球,据此估计该口袋中原有红色小球个数为 .
小明和同学做“抛掷质地均匀的硬币试验”获得的数据如表:
抛掷次数 |
100 |
200 |
300 |
400 |
500 |
正面朝上的频数 |
53 |
98 |
156 |
202 |
244 |
若抛掷硬币的次数为1000,则“正面朝上”的频数最接近
A.20B.300C.500D.800
在一个不透明的布袋中,红色、黑色、白色的球共有20个,除颜色外,形状、大小、质地等完全相同,小明通过大量摸球试验后发现摸到红色、黑色球的频率分别稳定在 和 ,则口袋中白色球的个数很可能是 个.
某校研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干名学生的兴趣爱好,并将调查结果绘制成下面两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
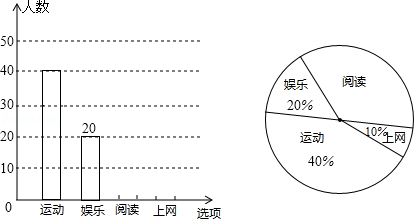
(1)在这次调查中,一共调查了 名学生;
(2)补全条形统计图;
(3)若该校共有1500名学生,估计爱好运动的学生有 人;
(4)在全校同学中随机选取一名学生参加演讲比赛,用频率估计概率,则选出的恰好是爱好阅读的学生的概率是 .
在一个不透明的口袋中,装有除颜色外无其他差别的4个白球和 个黄球.某同学进行了如下试验:从袋中随机摸出1个球记下它的颜色,放回摇匀,为一次摸球试验.记录摸球的次数与摸出白球的次数的列表如下:
摸球试验的次数 |
100 |
200 |
500 |
1000 |
摸出白球的次数 |
21 |
39 |
102 |
199 |
根据列表可以估计出 的值为 .
表中记录了某种苹果树苗在一定条件下移植成活的情况:
移植的棵数 |
200 |
500 |
800 |
2000 |
12000 |
成活的棵数 |
187 |
446 |
730 |
1790 |
10836 |
成活的频率 |
0.935 |
0.892 |
0.913 |
0.895 |
0.903 |
由此估计这种苹果树苗移植成活的概率约为 .(精确到
在一个不透明的箱子里装有红色、蓝色、黄色的球共20个,除颜色外,形状、大小、质地等完全相同,小明通过多次摸球实验后发现摸到红色、黄色球的频率分别稳定在 和 ,则箱子里蓝色球的个数很可能是 个.
下表记录了某种幼树在一定条件下移植成活情况
移植总数 |
400 |
1500 |
3500 |
7000 |
9000 |
14000 |
成活数 |
325 |
1336 |
3203 |
6335 |
8073 |
12628 |
成活的频率(精确到 ) |
0.813 |
0.891 |
0.915 |
0.905 |
0.897 |
0.902 |
由此估计这种幼树在此条件下移植成活的概率约是 (精确到 ).
新冠疫情期间,某校开展线上教学,有“录播”和“直播”两种教学方式供学生选择其中一种.为分析该校学生线上学习情况,在接受这两种教学方式的学生中各随机抽取40人调查学习参与度,数据整理结果如表(数据分组包含左端值不包含右端值).
参与度 人数 方式 |
|
|
|
|
录播 |
4 |
16 |
12 |
8 |
直播 |
2 |
10 |
16 |
12 |
(1)你认为哪种教学方式学生的参与度更高?简要说明理由.
(2)从教学方式为“直播”的学生中任意抽取一位学生,估计该学生的参与度在0.8及以上的概率是多少?
(3)该校共有800名学生,选择“录播”和“直播”的人数之比为 ,估计参与度在0.4以下的共有多少人?
一个不透明的袋中装有除颜色外均相同的9个红球,3个白球,若干个绿球,每次摇匀后随机摸出一个球,记下颜色后再放回袋中,经过大量重复实验后,发现摸到绿球的频率稳定在0.2,则袋中约有绿球 个.
某射手在相同条件下进行射击训练,结果如下:
射击次数 |
10 |
20 |
40 |
50 |
100 |
200 |
500 |
1000 |
击中靶心的频数 |
9 |
19 |
37 |
45 |
89 |
181 |
449 |
901 |
击中靶心的频率 |
0.900 |
0.950 |
0.925 |
0.900 |
0.890 |
0.905 |
0.898 |
0.901 |
该射手击中靶心的概率的估计值是 (精确到 .
扬州某毛绒玩具厂对一批毛绒玩具进行质量抽检的结果如下:
抽取的毛绒玩具数 |
20 |
50 |
100 |
200 |
500 |
1000 |
1500 |
2000 |
优等品的频数 |
19 |
47 |
91 |
184 |
462 |
921 |
1379 |
1846 |
优等品的频率 |
0.950 |
0.940 |
0.910 |
0.920 |
0.924 |
0.921 |
0.919 |
0.923 |
从这批玩具中,任意抽取的一个毛绒玩具是优等品的概率的估计值是 .(精确到