甲、乙两同学只有一张乒乓球比赛的门票,谁都想去,最后商定通过转盘游戏决定.游戏规则是:转动下面平均分成三个扇形且标有不同颜色的转盘,转盘连续转动两次,若指针前后所指颜色相同,则甲去;否则乙去.(如果指针恰好停在分割线上,那么重转一次,直到指针指向一种颜色为止)
(1)转盘连续转动两次,指针所指颜色共有几种情况?通过画树状图或列表法加以说明;
(2)你认为这个游戏公平吗?请说明理由.
两个不透明的袋子,一个装有两个球(1 个白球,一个红球),另一个装有3个球(1个白球,1个红球,1个绿球),小球除颜色不同外,其余完全相同.现从两个袋子中各随机摸出1个小球,两球颜色恰好相同的概率是 .
在阳光体育活动时间,小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球,当时只有一副空球桌,他们只能选两人打第一场.
(1)如果确定小亮打第一场,再从其余三人中随机选取一人打第一场,求恰好选中大刚的概率;
(2)如果确定小亮做裁判,用“手心、手背”的方法决定其余三人哪两人打第一场.游戏规则是:三人同时伸“手心、手背”中的一种手势,如果恰好有两人伸出的手势相同,那么这两人上场,否则重新开始,这三人伸出“手心”或“手背”都是随机的,请用画树状图的方法求小莹和小芳打第一场的概率.
在一个不透明的袋中装有除颜色外其余均相同的n个小球,其中有5个黑球,从袋中随机摸出一球,记下其颜色,这称为一次摸球试验,之后把它放回袋中,搅匀后,再继续摸出一球,以下是利用计算机模拟的摸球试验次数与摸出黑球次数的列表:
| 摸球试验次数 |
100 |
1000 |
5000 |
10000 |
50000 |
100000 |
| 摸出黑球次数 |
46 |
487 |
2506 |
5008 |
24996 |
50007 |
根据列表,可以估计出n的值是 .
从分别写有数字﹣4,﹣3,﹣2,﹣1,3,4的六张卡片中,任意抽取一张,则所抽卡片上数字的绝对值小于2的概率是( )
A. |
B. |
C. |
D. |
在一次课外活动中,李聪、何花、王军三位同学准备跳绳,他们约定用“抛硬币”的游戏方式来确定哪两位同学先用绳(如图1).

(1)请将如图2表示游戏一个回合所有可能出现结果的树状图补充完整;
(2)求一个回合能确定两位同学先用绳的概率.
在阳光体育活动时间,小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球,当时只有一副空球桌,他们只能选两人打第一场.
(1)如果确定小亮打第一场,再从其余三人中随机选取一人打第一场,求恰好选中大刚的概率;
(2)如果确定小亮做裁判,用“手心、手背”的方法决定其余三人哪两人打第一场.游戏规则是:三人同时伸“手心、手背”中的一种手势,如果恰好有两人伸出的手势相同,那么这两人上场,否则重新开始,这三人伸出“手心”或“手背”都是随机的,请用画树状图的方法求小莹和小芳打第一场的概率.
在一个不透明的袋中装有除颜色外其余均相同的n个小球,其中有5个黑球,从袋中随机摸出一球,记下其颜色,这称为一次摸球试验,之后把它放回袋中,搅匀后,再继续摸出一球,以下是利用计算机模拟的摸球试验次数与摸出黑球次数的列表:
| 摸球试验次数 |
100 |
1000 |
5000 |
10000 |
50000 |
100000 |
| 摸出黑球次数 |
46 |
487 |
2506 |
5008 |
24996 |
50007 |
根据列表,可以估计出n的值是 .
有7张正面分别标有数字 ,
, ,0,1,2,3,4的卡片,除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为m,则使关于x的方程
,0,1,2,3,4的卡片,除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为m,则使关于x的方程 有实数根,且使不等式组
有实数根,且使不等式组 无解的概率是 .
无解的概率是 .
《中国足球改革总体方案》提出足球要进校园.为了解某校学生对校园足球喜爱的情况,随机对该校部分学生进行了调查,将调查结果分为“很喜欢”、“较喜欢”、“一般”、“不喜欢”四个等级,并根据调查结果绘制成了如下两幅不完整的统计图:

(1)一共调查了 名学生,请补全条形统计图;
(2)在此次调查活动中,选择“一般”的学生中只有两人来自初三年级.现在要从选择“一般”的同学中随机抽选两人来谈谈各自对校园足球的感想,请用画树状图或列表法求选中的两人刚好都来自初三年级的概率.
在一只不透明的袋中,装着标有数字3,4,5,7的质地、大小均相同的小球,小明和小东同时从袋中随机各摸出1个球,并计算这两球上的数字之和,当和小于9时小明获胜,反之小东获胜.
(1)请用树状图或列表的方法,求小明获胜的概率;
(2)这个游戏公平吗?请说明理由.
同时投掷两个骰子,点数和为5的概率是( )
A.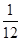 |
B.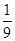 |
C. |
D. |