在一个不透明的口袋中，装有若干个除颜色不同其余都相同的球，如果口袋中装有4个红球且摸到红球的概率为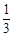
，那么口袋中球的总数为
| A．12个 | B．9个 | C．6个 | D．3个 |
如图是一个台球桌面的示意图，图中四个角上的阴影部分分别表示四个入球孔.若一个球按图中所示的方向被击出（球可以经过多次反射），则该球最后将落入的球袋是
| A．1 号袋 | B．2 号袋 | C．3 号袋 | D．4 号袋 |
在一个口袋中有3个完全相同的小球，把它们分别标号为1、2、3，随机地摸取一个小球后放回，再随机地摸出一个小球．求“两次取的小球的标号相同”的概率。请借助列表法或树形图说明理由。
一个口袋里有25个球，其中红球、黑球、黄球若干个，从口袋中随机摸出一球记下其颜色，再把它放回口袋中摇匀，重复上述过程，共试验200次，其中有120次摸到黄球，由此估计袋中的黄球有 个。
某同学想向班主任发短信拜年，可一时记不清班主任手机号码后三位数的顺序，只记得是1，6，9三个数字，则该同学一次发短信成功的概率是（ ）
A． |
B． |
C． |
D． |
某中学共有学生2000名，各年级男女生人数如下表：
| |
六年级 |
七年级 |
八年级 |
九年级 |
| 男生 |
250 |
z |
254 |
258 |
| 女生 |
x |
244 |
y |
252 |
若从全校学生中任意抽一名，抽到六年级女生的概率是0.12；若将各年级的男、女生人数制作成扇形统计图，八年级女生对应扇形的圆心角为44.28°．
（1）求x，y，z的值；
（2）求各年级男生的中位数；
（3）求各年级女生的平均数；
（4）从八年级随机抽取36名学生参加社会实践活动，求抽到八年级某同学的概率．
时代中学举行了一次科普知识竞赛.满分100分,学生得分的最低分31分．如图是根据学生竞赛成绩绘制的频数分布直方图的一部分．参加这次知识竞赛的学生共有40人，则得分在60~70分的频率为 
小明在白纸上任意画了一个锐角，他画的角在45º到60º之间的概率是
A． |
B． |
C． |
D． |
下图是由转盘和指针组成的装置
、
，两个转盘分别被分成三个面积相等的扇形. 装置上的数字分别是1，6，8，装置上的数字分别是4，5，7. 这两个装置除了表面数字不同外，其他构造完全相同. 现在你和另外一个同学分别同时用力转动装置、中的指针，如果我们规定指针停留在较大数字的一方获胜（若指针恰好停留在分界线上，则重新转动
一次，直到指针停留在某一数字为止），那么你选择的装置是 ，请说明理由．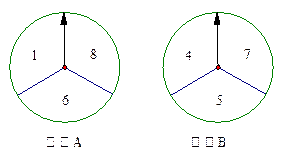
从一副扑克牌中取出1张红桃、2张黑桃共3张牌，将这3张牌洗匀后，从中任取1张牌恰好是黑桃的概率是 ．
下列事件中，必然事件是
| A．任意掷一枚均匀的硬币，正面朝上 |
| B．打开电视正在播放甲型H1N1流感的相关知识 |
| C．某射击运动员射击一次，命中靶心 |
| D．在只装有5个红球的袋中摸出1球，是红球 |
如图3，甲转盘被分成3个面积相等的扇形，乙转盘被分成2个面积相等的扇形．随机地转动指针(当指针指在边界线上时视为无效，重转)．
请解答下列问题．
⑴ 在图甲中，随机地转动指针，指针指向扇形2的概率是_____________；
⑵ 分别转动图甲和图乙的指针，两个指针停止时所指区域内的数之和为6或7，试用树状图或列表法求出其概率．
袋子中有2个红球，3个绿球和4个蓝球，它们只有颜色上的区别，从袋子中随机地抽取一个球是绿球的概率是
下列事件中，属于必然性事件的是 （ ）
| A．通常温度降到0℃以下，纯净的水结冰； |
| B．随意翻到一本书的某面，这页的页码是奇数； |
| C．购买一张彩票，中奖； |
| D．汽车累积行驶1万千米，从未出现故障． |
指针指向每个区域的可能性相等（不计指针与两个区域交线重合的情形），将所得区域的序号相乘，比较所得积为奇数和偶数的概率的大小。有人说：因为两个转盘中奇数序号比偶数序号多，显然所得积为奇数的概率大，你同意他的说法吗？请说明理由。
粤公网安备 44130202000953号