数学老师将全班分成7个小组开展小组合作学习,采用随机抽签确定一个小组进行展示活动,则第3个小组被抽到的概率是( )
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 的正方形网格中,有4个小正方形已经涂黑,若再涂黑任意1个白色的小正方形(每个白色小正方形被涂黑的可能性相同),使新构成的黑色部分图形是轴对称图形的概率是 .

从下列命题中,随机抽取一个是真命题的概率是
(1)无理数都是无限小数;
(2)因式分解 ;
(3)棱长是 的正方体的表面展开图的周长一定是 ;
(4)弧长是 ,面积是 的扇形的圆心角是 .
| A. |
|
B. |
|
C. |
|
D. |
1 |
现有五张正面图形分别是平行四边形、圆、等边三角形、正五边形、菱形的卡片,它们除正面图形不同,其它完全相同.将它们背面朝上洗匀后,从中随机抽取一张卡片,卡片的正面图形既是中心对称图形又是轴对称图形的概率是 .
下列说法正确的是
① 的值大于 ;
②正六边形的内角和是 ,它的边长等于半径;
③从一副扑克牌中随机抽取一张,它是黑桃的概率是 ;
④甲、乙两人各进行了10次射击测试,他们的平均成绩相同,方差分别是 , ,则乙的射击成绩比甲稳定.
| A. |
①②③④ |
B. |
①②④ |
C. |
①④ |
D. |
②③ |
一个不透明的口袋中有5个完全相同的小球,分别标号为1,2,3,4,5,从中随机摸出一个小球,其标号是偶数的概率为 .
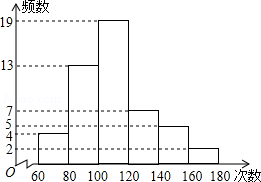
为了提高学生体质,战胜疫情,某中学组织全校学生宅家一分钟跳绳比赛,全校跳绳平均成绩是每分钟99次,某班班长统计了全班50名学生一分钟跳绳成绩,列出的频数分布直方图如图所示,(每个小组包括左端点,不包括右端点).
求:(1)该班一分钟跳绳的平均次数至少是多少,是否超过全校的平均次数;
(2)该班的一个学生说:“我的跳绳成绩是我班的中位数”请你给出该生跳绳成绩的所在范围;
(3)从该班中任选一人,其跳绳次数超过全校平均数的概率是多少.
在一个不透明的袋子中装有黑球 个、白球 个、红球3个,除颜色外无其它差别,任意摸出一个球是红球的概率是
| A. |
|
B. |
|
C. |
|
D. |
|
在,
,1,2,3五个数中随机选取一个数作为二次函数
中
的值,则该二次函数图象开口向上的概率是 .
某公司有甲、乙、丙三辆车去南京,它们出发的先后顺序随机.张先生和李先生乘坐该公司的车去南京出差,但有不同的需求.

请用所学概率知识解决下列问题:
(1)写出这三辆车按先后顺序出发的所有可能结果;
(2)两人中,谁乘坐到甲车的可能性大?请说明理由.
甲、乙两人去超市选购奶制品,有两个品牌的奶制品可供选购,其中蒙牛品牌有两个种类的奶制品: .纯牛奶, .核桃奶;伊利品牌有三个种类的奶制品: .纯牛奶, .酸奶, .核桃奶.
(1)甲从这两个品牌的奶制品中随机选购一种,选购到纯牛奶的概率是 ;
(2)若甲喜爱蒙牛品牌的奶制品,乙喜爱伊利品牌的奶制品,甲、乙两人从各自喜爱的品牌中随机选购一种奶制品,请利用画树状图或列表的方法求出两人选购到同一种类奶制品的概率.
在一个不透明的袋子中装有4个白球, 个红球.这些球除颜色外都相同.若从袋子中随机摸出1个球,摸到红球的概率为 ,则 .
如图,一个游戏转盘中,红、黄、蓝三个扇形的圆心角度数分别为 , , .让转盘自由转动,指针停止后落在黄色区域的概率是
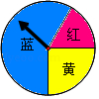
A. B. C. D.
某超市为庆祝开业举办大酬宾抽奖活动,凡在开业当天进店购物的顾客,都能获得一次抽奖的机会,抽奖规则如下:在一个不透明的盒子里装有分别标有数字1、2、3、4的4个小球,它们的形状、大小、质地完全相同,顾客先从盒子里随机取出一个小球,记下小球上标有的数字,然后把小球放回盒子并搅拌均匀,再从盒子中随机取出一个小球,记下小球上标有的数字,并计算两次记下的数字之和,若两次所得的数字之和为8,则可获得50元代金券一张;若所得的数字之和为6,则可获得30元代金券一张;若所得的数字之和为5,则可获得15元代金券一张;其他情况都不中奖.
(1)请用列表或树状图(树状图也称树形图)的方法(选其中一种即可),把抽奖一次可能出现的结果表示出来;
(2)假如你参加了该超市开业当天的一次抽奖活动,求能中奖的概率 .