2011年3月10日，云南省发生了5.8级地震，我区某中学开展了“情系云南，大爱无疆”爱心捐款活动．团干部对九（1）班的捐款情况进行了统计，并把统计的结果制作了一个不完全的频数分布直方图和扇形统计图．已知学生捐款最少的是5元，最多的不足25元．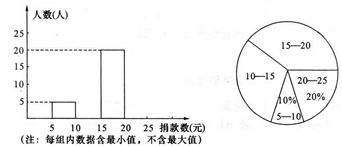
请补全频数分布直方图
九（1）班学生捐款的中位数所在的组别范围是＿＿＿＿；
九（1）班学生小明捐款24元，班主任拟在捐款最多的20－25元这组同学中随机选取一人代表班级在学校组织的爱心活动大会上发言，小明同学被选中的概率是＿＿＿＿．
某中学对全校学生进行文明礼仪知识测试，为了解测试结果，随机抽取部分学生的成绩进行分析，将成绩分为三个等级：不合格、一般、优秀，并绘制成如下两幅统计图（不完整）．请你根据图中所给的信息解答下列问题：
（1）请将以上两幅统计图补充完整（扇形统计图填上“一般”的百分率，条形统计图上画出“优秀”的条形图）；
（2）若“一般”和“优秀”均被视为达标成绩，则该校被抽取的学生中有 人达标；
（3）若该校学生有1200人，请你估计此次测试中，全校达标的学生有多少人？
(本题6分)为了考察甲、乙两种小麦的长势，分别从中抽出10株苗，测得苗高如下（单位：cm）：
| 甲 |
11 |
15 |
11 |
13 |
16 |
10 |
15 |
14 |
13 |
12 |
| 乙 |
16 |
10 |
8 |
6 |
19 |
13 |
14 |
17 |
16 |
11 |
（1）计算甲、乙两种小麦苗高的平均数；
（2）计算甲、乙两种小麦苗高的方差，并判断哪种小麦长得比较整齐？
现有7名同学测得某大厦的高度如下：（单位：m）
29.8 30.0 30.0 30.0 30.2 44.0 30.0（1）在这组数据中，中位数是_____________，众数是_____________，平均数是_____________；
（2）凭经验，你觉得
此大厦大概有多高？请简要
说明理由。
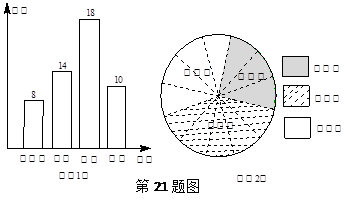
国家教育部规定“中小学生每天在校体育活动时间不低于1小时”．某中学为了了解学生体育活动情况，随机抽查了520名毕业班学生，调查内容是：“每天锻炼是否超过1小时及未超过1小时的原因”．以下是根据所得的数据制成的统计图的一部分．
根据以上信息，解答下列问题：每天在校锻炼时间超过1小时的人数是 ；
请将图2补充完整；
2010年我市初中毕业生约为9.6万人，请你估计今年全市初中毕业生中每天锻炼时间超过1小时的学生约有多少万人？
宣传交通安全知识，争做安全小卫士．某校进行“交通安全知识”宣传培训后进行了一次测试．学生考分按标准划分为不合格、合格、良好、优秀四个等级，为了解全校的考试情况，对在校的学生随机抽样调查，得到图（1）的条形统计图，请结合统计图回答下列问题：该校抽样调查的学生人数为_______名；抽样中考生分数的中位数所在等级是________；
抽样中不及格的人数是多少？占被调查人数的百分比是多少？
若已知该校九年级有学生500名，图（2）是各年级人数占全校人数百分比的扇形图（图中圆心角被等分），请你估计全校优良（良好与优秀）的人数约有多少人？
在学习“数据的收集与简单统计图”这一章节时，前进中学曾经要求同学们做过“同学上学方式”的调查。如图是前进中学七年级（3）班同学上学方式的条形统计图。
（1）前进中学七年级（3）班共有_______名学生；
（2）请你改用扇形统计图来表示前进中学七年级（3）班同学上学方式；
（3）从统计图中你可以获得哪些信息?
甲、乙两名同学进行射击训练，在相同条件下各射靶5次，成绩统计如下：
| 命中环数 |
7 |
8 |
9 |
10 |
| 甲命中环数的次数 |
2 |
2 |
0 |
1 |
| 乙命中环数的次 |
1 |
3 |
1 |
0 |
若从甲、乙两人射击成绩方差的角度评价两人的射击水平，则谁的射击成绩更稳定
些？
某区教育局为了了解学生参加阳光体育活动的情况，对某校学生进行随机抽样
调查，其中一个问题是“你平均每天参加阳光体育活动的时间是多少?”，共有4个选项：
A．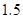
小时以上 B．
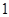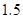～小时 C．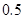
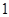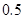～小时 D．小时以下
图1、2是根据调查结果绘制的两幅不完整的统计图，
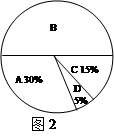
请你根据统计图提供的信息，解答以下问题：
(1)本次一共调查了多少名学生?
(2)在图
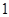中将选项B的部分补充完整； (3)若该校有
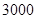名学生，你估计全校可能有多少名学
生平均每天参加体育活动的时间在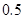小时以下．
在一次投篮比赛中，甲、乙两人共进行五轮比赛，每轮各投10个球，他们每轮投中的球数如下表：
| 轮次 |
一 |
二 |
三 |
四 |
五 |
| 甲投中（个） |
6 |
8 |
7 |
5 |
9 |
| 乙投中（个） |
7 |
8 |
6 |
7 |
7 |
请你计算甲、乙两人投篮的平均数.
从统计学的角度考虑，通过计算，你认为在比赛中甲、乙两人谁的发挥更稳定些？
某区教育局为了了解学生参加阳光体育活动的情况，对某校学生进行随机抽样
调查，其中一个问题是“你平均每天参加阳光体育活动的时间是多少?”，共有4个选项： 
A． 小时以上 |
B． ～小时 |
C． ～小时 |
D．小时以下 |
图1、2是根据调查结果绘制的两幅不完整的统计图，
请你根据统计图提供的信息，解答以下问题：
(1)本次一共调查了多少名学生?
(2)在图中将选项B的部分补充完整； 
(3)若该校有
名学生，你估计全校可能有多少名学
生平均每天参加体育活动的时间在小时以下．
．如下的两幅不完整的统计图反映了重庆一中校男子篮球队的年龄分布情况：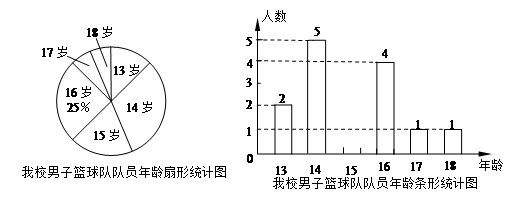
请根据图中提供的信息，解答下列问题：
（1）重庆一中校男子篮球队队员有多少人？
（2）将条形统计图补充完整；
（3）在扇形统计图中，求出“15岁”部分所对应的圆心角的度数；
（4）重庆一中校男子篮球队队员的平均年龄是多少？
：某学校举行演讲比赛，选出了10名同学担任评委，并事先拟定从以下4个方案中选择合理的方案来确定每个演讲者的最后得分。
方案1：所有评委所给分的平均数．方案2：在所有评委所给分中，去掉一个最高分和一个最低分，然后再计算其余给分的平均数．
方案3：所有评委所给分的中位数．
方案4：所有评委所给分的众数．
|
为了探究上述方案的合理性，先对某个同学的演讲成绩进行了统计实验．下面是这个同学的得分统计图：
如图，点A、O、B在同一条直线上
（1）∠AOC比∠BOC大100°，求∠AOC与∠BOC的度数
（2）在(1)的条件下，若∠BOC与∠BOD互余，求∠BOD的度数
（3）在（2）的条件下，若OE平分∠AOC，求∠DOE的度数
(本题满分12分) 为了让广大青少年学生走向操场，走进自然，走到阳光下，积极参加体育锻炼，我国启动了“全国亿万学生阳光体育运动”．短跑运动可以锻炼人的灵活性，增强人的爆发力．因此小明和小亮在课外活动中报名参加了短跑训练小组．在近几次百米训练中，所测成绩如图所示，请根据图中所示解答以下问题．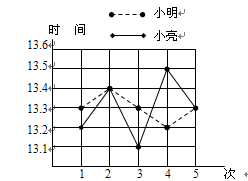
（1）请根据图中信息，补齐下面的表格；
| |
第1次 |
第2次 |
第3次 |
第4次 |
第5次 |
| 小明 |
13.3 |
13.4 |
13.3 |
|
13.3 |
| 小亮 |
13.2 |
|
13.1 |
13.5 |
13.3 |
（2）分别计算他们的平均数、极差和方差填入下表，若你是他们的教练，将小明与小亮的成绩比较后，你将分别给予他们怎样的建议？
| |
平均数 |
极差 |
方差 |
| 小明 |
13.3 |
|
0.004 |
| 小亮 |
|
0.4 |
|
粤公网安备 44130202000953号