初中数学加权平均数试题

某公司员工的月工资如下：

员工	经理	副经理	职员 $A$	职员 $B$	职员 $C$	职员 $D$	职员 $E$	职员 $F$	杂工 $G$
月工资 $/$元	7000	4400	2400	2000	1900	1800	1800	1800	1200

经理、职员 $C$、职员 $D$从不同的角度描述了该公司员工的收入情况．

设该公司员工的月工资数据（见上述表格）的平均数、中位数、众数分别为 $k$、 $m$、 $n$，请根据上述信息完成下列问题：

（1） $k=$　 　， $m=$　　， $n=$　　；

（2）上月一个员工辞职了，从本月开始，停发该员工工资，若本月该公司剩下的8名员工的月工资不变，但这8名员工的月工资数据（单位：元）的平均数比原9名员工的月工资数据（见上述表格）的平均数减小了．你认为辞职的那名员工可能是　　．

某公司员工的月工资如下：

员工	经理	副经理	职员 $A$	职员 $B$	职员 $C$	职员 $D$	职员 $E$	职员 $F$	杂工 $G$
月工资 $/$元	7000	4400	2400	2000	1900	1800	1800	1800	1200

经理、职员 $C$、职员 $D$从不同的角度描述了该公司员工的收入情况．

设该公司员工的月工资数据（见上述表格）的平均数、中位数、众数分别为 $k$、 $m$、 $n$，请根据上述信息完成下列问题：

（1） $k=$　 　， $m=$　　， $n=$　　；

（2）上月一个员工辞职了，从本月开始，停发该员工工资，若本月该公司剩下的8名员工的月工资不变，但这8名员工的月工资数据（单位：元）的平均数比原9名员工的月工资数据（见上述表格）的平均数减小了．你认为辞职的那名员工可能是　　．

王大伯承包了一个鱼塘，投放了2000条某种鱼苗，经过一段时间的精心喂养，存活率大致达到了 $90\%$．他近期想出售鱼塘里的这种鱼．为了估计鱼塘里这种鱼的总质量，王大伯随机捕捞了20条鱼，分别称得其质量后放回鱼塘．现将这20条鱼的质量作为样本，统计结果如图所示：

（1）这20条鱼质量的中位数是　　，众数是　　．

（2）求这20条鱼质量的平均数；

（3）经了解，近期市场上这种鱼的售价为每千克18元，请利用这个样本的平均数．估计王大伯近期售完鱼塘里的这种鱼可收入多少元？

某家庭记录了未使用节水龙头20天的日用水量数据（单位： $m^3)$和使用了节水龙头20天的日用水量数据，得到频数分布表如下：

未使用节水龙头20天的日用水量频数分布表：

日用水量 $/m^3$	$0⩽x<0.1$	$0.1⩽x<0.2$	$0.2⩽x<0.3$	$0.3⩽x<0.4$	$0.4⩽x<0.5$
频数	0	4	2	4	10

使用了节水龙头20天的日用水量频数分布表：

日用水量 $/m^3$	$0⩽x<0.1$	$0.1⩽x<0.2$	$0.2⩽x<0.3$	$0.3⩽x<0.4$
频数	2	6	8	4

（1）计算未使用节水龙头20天的日平均用水量和使用了节水龙头20天的日平均用水量；

（2）估计该家庭使用节水龙头后，一年能节省多少立方米水？（一年按365天计算）

小明为了解本班同学一周的课外阅读量，随机抽取班上15名同学进行调查，并将调查结果绘制成折线统计图（如图），则下列说法正确的是 $($　　 $)$

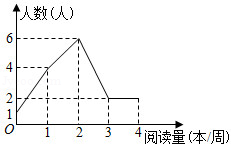
A．中位数是3，众数是2B．众数是1，平均数是2

C．中位数是2，众数是2D．中位数是3，平均数是2.5

某市从不同学校随机抽取100名初中生，对“学校统一使用数学教辅用书的册数”进行调查，统计结果如下：

册数	0	1	2	3
人数	13	35	29	23

关于这组数据，下列说法正确的是 $($　　 $)$

A．众数是2册B．中位数是2册C．极差是2册D．平均数是2册

某商场为了解产品 $A$的销售情况，在上个月的销售记录中，随机抽取了5天 $A$产品的销售记录，其售价 $x$（元 $/$件）与对应销量 $y$（件 $)$的全部数据如下表：

售价 $x$（元 $/$件）	90	95	100	105	110
销量 $y$（件 $)$	110	100	80	60	50

则这5天中， $A$产品平均每件的售价为 $($　　 $)$

A．100元B．95元C．98元D．97.5元

某市教育局组织全市中小学教师开展“请千家”活动．活动过程中，教有局随机抽取了近两周家访的教师人数及家访次数，将采集到的全部数据按家访次数分成五类，由甲、乙两人分别绘制了下面的两幅统计图（图都不完整）．

请根据以上信息，解答下列问题：

（1）请把这幅条形统计图补充完整（画图后请标注相应的数据）；

（2）在采集到的数据中，近两周平均每位教师家访　　次；

（3）若该市有12000名教师，则近两周家访不少于3次的教师约有　　人．

某商场服装部为了调动营业员的积极性，决定实行目标管理，根据目标完成的情况对营业员进行适当的奖励．为了确定一个适当的月销售目标，商场服装部统计了每位营业员在某月的销售额（单位：万元），数据如下：

17	18	16	13	24	15	28	26	18	19
22	17	16	19	32	30	16	14	15	26
15	32	23	17	15	15	28	28	16	19

对这30个数据按组距3进行分组，并整理、描述和分析如下．

频数分布表

组别	一	二	三	四	五	六	七
销售额	$13⩽x<16$	$16⩽x<19$	$19⩽x<22$	$22⩽x<25$	$25⩽x<28$	$28⩽x<31$	$31⩽x<34$
频数	7	9	3	$a$	2	$b$	2

数据分析表

平均数	众数	中位数
20.3	$c$	18

请根据以上信息解答下列问题：

（1）填空： $a=$　　， $b=$　　， $c=$　　；

（2）若将月销售额不低于25万元确定为销售目标，则有　　位营业员获得奖励；

（3）若想让一半左右的营业员都能达到销售目标，你认为月销售额定为多少合适？说明理由．

4月23日是世界读书日，习近平总书记说：“读书可以让人保持思想活力，让人得到智慧启发，让人滋养浩然之气．”某校响应号召，鼓励师生利用课余时间广泛阅读．该校文学社为了解学生课外阅读情况，抽样调查了部分学生每周用于课外阅读的时间，过程如下：

数据收集：从全校随机抽取20名学生，进行了每周用于课外阅读时间的调查，数据如下（单位： $\mathit{min})$

30	60	81	50	40	110	130	146	90	100
60	81	120	140	70	81	10	20	100	81

整理数据：按如下分段整理样本数据并补全表格：

课外阅读时间 $x\left(\mathit{min}\right)$	$0⩽x<40$	$40⩽x<80$	$80⩽x<120$	$120⩽x<160$
等级	$D$	$C$	$B$	$A$
人数	3		8

分析数据：补全下列表格中的统计量：

平均数	中位数	众数
80

得出结论：

（1）用样本中的统计量估计该校学生每周用于课外阅读时间的情况等级为　　；

（2）如果该校现有学生400人，估计等级为“ $B$”的学生有多少名？

（3）假设平均阅读一本课外书的时间为160分钟，请你选择样本中的一种统计量估计该校学生每人一年（按52周计算）平均阅读多少本课外书？

为了解某地区机动车拥有量对道路通行的影响，学校九年级社会实践小组对2010年 $~2017$年机动车拥有量、车辆经过人民路路口和学校门口的堵车次数进行调查统计，并绘制成下列统计图：

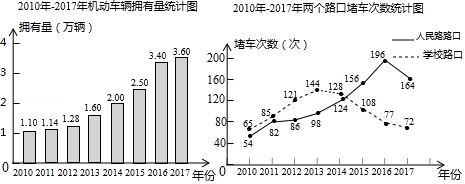
根据统计图，回答下列问题：

（1）写出2016年机动车的拥有量，分别计算2010年 $~2017$年在人民路路口和学校门口堵车次数的平均数．

（2）根据统计数据，结合生活实际，对机动车拥有量与人民路路口和学校门口堵车次数，说说你的看法．

10名学生的平均成绩是 $x$，如果另外5名学生每人得84分，那么整个组的平均成绩是 $($　　 $)$分

A． $\frac{x+84}{2}$B． $\frac{10x+420}{15}$C． $\frac{10x+84}{15}$D． $\frac{10+420}{15}$

为积极创建全国文明城市，某市对某路口的行人交通违章情况进行了20天的调查，将所得数据绘制成如下统计图（图2不完整） $:$

请根据所给信息，解答下列问题：

（1）第7天，这一路口的行人交通违章次数是多少次？这20天中，行人交通违章6次的有多少天？

（2）请把图2中的频数直方图补充完整；（温馨提示：请画在答题卷相对应的图上）

（3）通过宣传教育后，行人的交通违章次数明显减少．经对这一路口的再次调查发现，平均每天的行人交通违章次数比第一次调查时减少了4次，求通过宣传教育后，这一路口平均每天还出现多少次行人的交通违章？

有甲、乙、丙三种糖果混合而成的什锦糖100千克，其中各种糖果的单价和千克数如表所示，商家用加权平均数来确定什锦糖的单价．

	甲种糖果	乙种糖果	丙种糖果
单价（元 $/$千克）	15	25	30
千克数	40	40	20

（1）求该什锦糖的单价．

（2）为了使什锦糖的单价每千克至少降低2元，商家计划在什锦糖中加入甲、丙两种糖果共100千克，问其中最多可加入丙种糖果多少千克？

某中学随机地调查了50名学生，了解他们一周在校的体育锻炼时间，结果如下表所示：

时间（小时）	5	6	7	8
人数	10	15	20	5

则这50名学生这一周在校的平均体育锻炼时间是　　小时．