初中数学用样本估计总体试题

我市于2021年5月 $22-23$日在遂宁观音湖举行了“龙舟赛”，吸引了全国各地选手参加．现对某校初中1000名学生就“比赛规则”的了解程度进行了抽样调查（参与调查的同学只能选择其中一项），并将调查结果绘制出两幅不完整的统计图表，请根据统计图表回答下列问题：

类别	频数	频率
不了解	10	$m$
了解很少	16	0.32
基本了解	$b$
很了解	4	$n$
合计	$a$	1

（1）根据以上信息可知： $a=$　　， $b=$　　， $m=$　　， $n=$　　；

（2）补全条形统计图；

（3）估计该校1000名初中学生中“基本了解”的人数约有　　人；

（4）“很了解”的4名学生是三男一女，现从这4人中随机抽取两人去参加全市举办的“龙舟赛”知识竞赛，请用画树状图或列表的方法说明，抽到两名学生均为男生和抽到一男一女的概率是否相同．

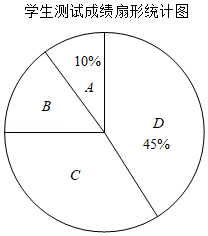
为了解某校九年级学生的体质健康状况，随机抽取了该校九年级学生的 $10\%$进行测试，将这些学生的测试成绩 $\left(x\right)$分为四个等级：优秀 $85⩽x⩽100$；良好 $75⩽x<85$；及格 $60⩽x<75$；不及格 $0⩽x<60$，并绘制成如图两幅统计图．

根据以上信息，解答下列问题：

（1）在抽取的学生中不及格人数所占的百分比是　     ；

（2）计算所抽取学生测试成绩的平均分；

（3）若不及格学生的人数为2人，请估算出该校九年级学生中优秀等级的人数．

为加强交通安全教育，某中学对全体学生进行“交通知识”测试，学校随机抽取了部分学生的测试成绩，并根据测试成绩绘制两种统计图表（不完整），请结合图中信息解答下列问题：

学生测试成绩频数分布表

组别	成绩 $x$分	人数
$A$	$60⩽x<70$	8
$B$	$70⩽x<80$	$m$
$C$	$80⩽x<90$	24
$D$	$90⩽x⩽100$	$n$

（1）表中的 $m$值为 　　， $n$值为 　　；

（2）求扇形统计图中 $C$部分所在扇形的圆心角度数；

（3）若测试成绩80分以上（含80分）为优秀，根据调查结果请估计全校2000名学生中测试成绩为优秀的人数．

某鞋店在一周内销售某款女鞋，尺码（单位： $\mathit{cm})$数据收集如下：

24	23.5	21.5	23.5	24.5	23	22	23.5	23.5	23	22.5	23.5	23.5	22.5	24
24	22.5	25	23	23	23.5	23	22.5	23	23.5	23.5	23	24	22	22.5

绘制如图不完整的频数分布表及频数分布直方图：

尺码 $/\mathit{cm}$	划记	频数
$21.5⩽x<22.5$		3
$22.5⩽x<23.5$
$23.5⩽x<24.5$		13
$24.5⩽x<25.5$		2

（1）请补全频数分布表和频数分布直方图；

（2）若店主要进货，她最应该关注的是尺码的众数，上面数据的众数为　　；

（3）若店主下周对该款女鞋进货120双，尺码在 $23.5⩽x<25.5$范围的鞋应购进约多少双？

某市为了解八年级学生视力健康状况，在全市随机抽查了400名八年级学生2021年初的视力数据，并调取该批学生2020年初的视力数据，制成如图统计图（不完整） $:$

青少年视力健康标准

类别	视力	健康状况
$A$	视力     $⩾5.0$	视力正常
$B$	4.9	轻度视力不良
$C$	$4.6⩽$ 视力     $⩽4.8$	中度视力不良
$D$	视力     $⩽4.5$	重度视力不良

根据以上信息，请解答：

（1）分别求出被抽查的400名学生2021年初轻度视力不良（类别 $B)$ 的扇形圆心角度数和2020年初视力正常（类别 $A)$ 的人数．

（2）若2021年初该市有八年级学生2万人，请估计这些学生2021年初视力正常的人数比2020年初增加了多少人？

（3）国家卫健委要求，全国初中生视力不良率控制在 $69\%$ 以内．请估计该市八年级学生2021年初视力不良率是否符合要求？并说明理由．

王大伯承包了一个鱼塘，投放了2000条某种鱼苗，经过一段时间的精心喂养，存活率大致达到了 $90\%$．他近期想出售鱼塘里的这种鱼．为了估计鱼塘里这种鱼的总质量，王大伯随机捕捞了20条鱼，分别称得其质量后放回鱼塘．现将这20条鱼的质量作为样本，统计结果如图所示：

（1）这20条鱼质量的中位数是　　，众数是　　．

（2）求这20条鱼质量的平均数；

（3）经了解，近期市场上这种鱼的售价为每千克18元，请利用这个样本的平均数．估计王大伯近期售完鱼塘里的这种鱼可收入多少元？

某校开展了"禁毒"知识的宣传教育活动．为了解这次活动的效果，现随机抽取部分学生进行知识测试，并将所得数据绘制成不完整的统计图表．

等级	频数（人数）	频率
优秀	60	0.6
良好	$a$	0.25
合格	10	$b$
基本合格	5	0.05
合计	$c$	1

根据统计图表提供的信息，解答下列问题：

（1） $a=$ 　　， $b=$ 　　， $c=$ 　　；

（2）补全条形统计图；

（3）该学校共有1600名学生，估计测试成绩等级在合格以上（包括合格）的学生约有多少人？

（4）在这次测试中，九年级（3）班的甲、乙、丙、丁四位同学的成绩均为"优秀"，现班主任准备从这四名同学中随机选取两名同学出一期"禁毒"知识的黑板报，请用列表法或画树状图法求甲、乙两名同学同时被选中的概率．

某家庭记录了未使用节水龙头20天的日用水量数据（单位： $m^3)$和使用了节水龙头20天的日用水量数据，得到频数分布表如下：

未使用节水龙头20天的日用水量频数分布表：

日用水量 $/m^3$	$0⩽x<0.1$	$0.1⩽x<0.2$	$0.2⩽x<0.3$	$0.3⩽x<0.4$	$0.4⩽x<0.5$
频数	0	4	2	4	10

使用了节水龙头20天的日用水量频数分布表：

日用水量 $/m^3$	$0⩽x<0.1$	$0.1⩽x<0.2$	$0.2⩽x<0.3$	$0.3⩽x<0.4$
频数	2	6	8	4

（1）计算未使用节水龙头20天的日平均用水量和使用了节水龙头20天的日平均用水量；

（2）估计该家庭使用节水龙头后，一年能节省多少立方米水？（一年按365天计算）

某中学全校师生听取了"禁毒"宣传报告后，对禁毒人员肃然起敬．学校德育处随后决定在全校1000名学生中开展"我为禁毒献爱心"的捐款活动．张老师在周五随机调查了部分学生随身携带零花钱的情况，并将收集的数据进行整理，绘制了如图所示的条形统计图．

（1）求这组数据的平均数和众数；

（2）经调查，当学生身上的零花钱多于15元时，都愿捐出零花钱的 $20\%$ ，其余学生不参加捐款．请你估计周五这一天该校可能收到学生自愿捐款多少元？

（3）捐款最多的两人将和另一个学校选出的两人组成一个"禁毒"知识宣讲小组，若从4人中随机指定两人担任正、副组长，求这两人来自不同学校的概率．

某校开展主题为"防疫常识知多少"的调查活动，抽取了部分学生进行调查，调查问卷设置了 $A$ ：非常了解、 $B$ ：比较了解、 $C$ ：基本了解、 $D$ ：不太了解四个等级，要求每个学生填且只能填其中的一个等级，采取随机抽样的方式，并根据调查结果绘制成如图所示不完整的频数分布表和频数分布直方图，根据以上信息回答下列问题：

等级	频数	频率
$A$	20	0.4
$B$	15	$b$
$C$	10	0.2
$D$	$a$	0.1

（1）频数分布表中 $a=$ 　　， $b=$ 　　，将频数分布直方图补充完整；

（2）若该校有学生1000人，请根据抽样调查结果估算该校"非常了解"和"比较了解"防疫常识的学生共有多少人？

（3）在"非常了解"防疫常识的学生中，某班有5个学生，其中3男2女，计划在这5个学生中随机抽选两个加入防疫志愿者团队，请用列表或画树状图的方法求所选两个学生中至少有一个女生的概率．

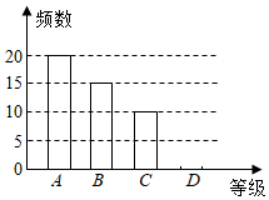
2021年是中国共产党建党100周年，某校开展了全校教师学习党史活动并进行了党史知识竞赛，从七、八年级中各随机抽取了20名教师，统计这部分教师的竞赛成绩（竞赛成绩均为整数，满分为10分，9分及以上为优秀）．相关数据统计、整理如下：

抽取七年级教师的竞赛成绩（单位：分） $:$

6，7，7，8，8，8，8，8，8，8，8，9，9，9，9，10，10，10，10，10．

七八年级教师竞赛成绩统计表

年级	七年级	八年级
平均数	8.5	8.5
中位数	$a$	9
众数	8	$b$
优秀率	$45\%$	$55\%$

根据以上信息，解答下列问题：

（1）填空： $a=$ 　　， $b=$ 　　；

（2）估计该校七年级120名教师中竞赛成绩达到8分及以上的人数；

（3）根据以上数据分析，从一个方面评价两个年级教师学习党史的竞赛成绩谁更优异．

绍兴莲花落，又称"莲花乐"，"莲花闹"，是绍兴一带的曲艺．为了解学生对该曲种的熟悉度，某校设置了：非常了解、了解、了解很少、不了解四个选项，随机抽查了部分学生进行问卷调查，要求每名学生只选其中的一项，并将抽查结果绘制成不完整的统计图．

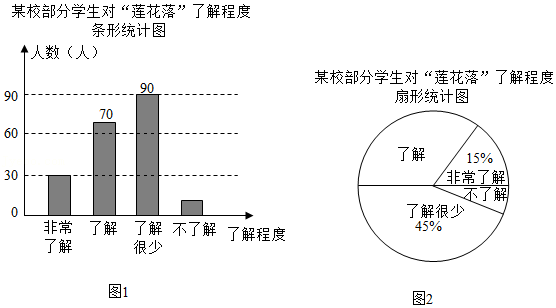
根据图中信息，解答下列问题：

（1）本次接受问卷调查的学生有多少人？并求图2中"了解"的扇形圆心角的度数；

（2）全校共有1200名学生，请你估计全校学生中"非常了解"、"了解"莲花落的学生共有多少人．

某校为了增强学生的疫情防控意识，组织全校2000名学生进行了疫情防控知识竞赛．从中随机抽取了 $n$ 名学生的竞赛成绩（满分100分），分成四组： $A:60⩽x<70$ ； $B:70⩽x<80$ ； $C:80⩽x<90$ ； $D:90⩽x⩽100$ ，并绘制出不完整的统计图：

（1）填空： $n=$ 　　；

（2）补全频数分布直方图；

（3）抽取的这 $n$ 名学生成绩的中位数落在 　　组；

（4）若规定学生成绩 $x⩾90$ 为优秀，估算全校成绩达到优秀的人数．

为有效推进儿童青少年近视防控工作，教育部办公厅等十五部门联合制定《儿童青少年近视防控光明行动工作方案 $(2021-2025$年）》，共提出八项主要任务，其中第三项任务为强化户外活动和体育锻炼．我市各校积极落实方案精神，某学校决定开设以下四种球类的户外体育选修课程：篮球、足球、排球、乒乓球．为了解学生需求，该校随机对本校部分学生进行了“你选择哪种球类课程”的调查（要求必须选择且只能选择其中一门课程），并根据调查结果绘制成不完整的统计图表．

课程	人数
篮球	$m$
足球	21
排球	30
乒乓球	$n$

根据图表信息，解答下列问题：

（1）分别求出表中 $m$， $n$的值；

（2）求扇形统计图中“足球”对应的扇形圆心角的度数；

（3）该校共有2000名学生，请你估计其中选择“乒乓球”课程的学生人数．

为庆祝中国共产党建党100周年，某校开展了"党在我心中"党史知识竞赛，竞赛得分为整数，王老师为了解竞赛情况，随机抽取了部分参赛学生的得分并进行整理，绘制成不完整的统计图表．

组别	成绩 $x$ （分 $)$	频数
$A$	$75.5⩽x<80.5$	6
$B$	$80.5⩽x<85.5$	14
$C$	$85.5⩽x<90.5$	$m$
$D$	$90.5⩽x<95.5$	$n$
$E$	$95.5⩽x<100.5$	$p$

请你根据统计图表提供的信息解答下列问题：

（1）上表中的 $m=$ 　　， $n=$ 　　， $p=$ 　　．

（2）这次抽样调查的成绩的中位数落在哪个组？请补全频数分布直方图．

（3）已知该校有1000名学生参赛，请估计竞赛成绩在90分以上的学生有多少人？

（4）现要从 $E$ 组随机抽取两名学生参加上级部门组织的党史知识竞赛， $E$ 组中的小丽和小洁是一对好朋友，请用列表或画树状图的方法求出恰好抽到小丽和小洁的概率．