已知点P是△ABC内一点,且它到三角形的三个顶点距离之和最小,则P点叫△ABC的费马点(Fermat point).已经证明:在三个内角均小于120°的△ABC中,当 时,P就是△ABC的费马点.若点P是腰长为 的等腰直角三角形DEF的费马点,则 .
如果三角形有一边上的中线长等于这边的长,那么称这个三角形为"好玩三角形".若Rt△ ABC是"好玩三角形",且∠ A=90°,则tan∠ ABC= .
两个全等的三角尺重叠放在△ACB的位置,将其中一个三角尺绕着点C按逆时针方向旋转至△DCE的位置,使点A恰好落在边DE上,AB与CE相交于点F.已知∠ACB=∠DCE=90°,∠B=30°,AB=8cm,则CF= cm.
如图,AB=6,O是AB的中点,直线l经过点O,∠1=120°,P是直线l上一点,当△APB为直角三角形时,AP= .

如图,直线 y=﹣ x﹣ 与 x, y轴分别交于点 A, B,与反比例函数 y= 的图象在第二象限交于点 C,过点 A作 x轴的垂线交该反比例函数图象于点 D.若 AD= AC,则点 D的坐标为 .

如图,在▱ ABCD中,∠ B=30°, AB= AC, O是两条对角线的交点,过点 O作 AC的垂线分别交边 AD, BC于点 E, F;点 M是边 AB的一个三等分点,则△ AOE与△ BMF的面积比为 .
如图,以边长为20 cm的正三角形铁皮的各顶点为端点,在各边上分别截取6 cm长的六条线段,过截得的六个端点作所在边的垂线,形成三个有两个直角的四边形.把它们沿虚线剪掉,用剩下的纸板折成一个底为正三角形的无盖柱形盒子,则这个盒子的容积为 cm 3.

如图,在Rt△ ABC中,∠ B=90°, AB= BC=2,将△ ABC绕点 C顺时针旋转60°,得到△ DEC,则 AE的长是 .

如图,正方形ABCO的顶点C、A分别在x轴、y轴上,BC是菱形BDCE的对角线,若∠D=60°,BC=2,则点D的坐标是 .
如图,在矩形 中,
中, ,以顶点
,以顶点 为圆心,1为半径作
为圆心,1为半径作 ,过边
,过边 上的一点
上的一点 作射线
作射线 与
与 相切于点
相切于点 ,且交边
,且交边 于点
于点 ,连接
,连接 ,若
,若 ,
, ,则
,则 的大小约为 度 分.(参考数据:
,
)
的大小约为 度 分.(参考数据:
,
)

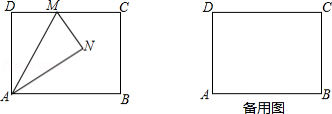
如图,矩形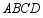 中,
中,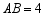 ,
, ,
,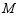 是边
是边 上一点,将
上一点,将 沿直线
沿直线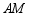 对折,得到
对折,得到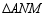 .
.
(1)当 平分
平分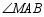 时,求
时,求 的长;
的长;
(2)连接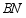 ,当
,当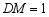 时,求
时,求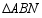 的面积;
的面积;
(3)当射线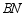 交线段
交线段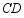 于点
于点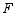 时,求
时,求 的最大值.
的最大值.
如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角 为
为 ,
, ,
, ,
, 都在格点上,则
都在格点上,则 的值是 .
的值是 .

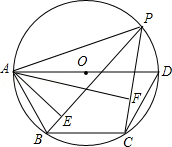
如图,点 P是四边形 ABCD外接圆上任意一点,且不与四边形顶点重合,若 AD是⊙ O的直径, AB= BC= CD.连接 PA、 PB、 PC,若 PA= a,则点 A到 PB和 PC的距离之和 AE+ AF= .