（1）解不等式组
并把解集在数轴上表示出来；
（2）如图，已知墙高AB为6.5米，将一长为6米的梯子CD斜靠在墙面，梯子与地面所成的角∠BCD=55°，此时梯子的顶端与墙顶的距离AD为多少米？（结果精确到0.1米）（参考数据：sin55°≈0.82，cos55°≈0.57，tan55°≈1.43）
如图，小明在楼上点A处测量大树的高，在A处测得大树顶部B的仰角为25°，测得大树底部C的俯角为45°．已知点A距地面的高度AD为12m，求大树的高度BC．（最后结果精确到0.1）
如图，岸边的点A处距水面的高度AB为2.17米，桥墩顶部点C距水面的高度CD为23.17米．从点A处测得桥墩顶部点C的仰角为26°，求岸边的点A与桥墩顶部点C之间的距离．（结果精确到0.1米）（参考数据：sin26°=0.44，cos26°=0.90，tan26°=0.49）
如图，某公司入口处有一斜坡AB，坡角为12°，AB的长为3m，施工队准备将斜坡修成三级台阶，台阶高度均为hcm，深度均为30cm，设台阶的起点为C．
（1）求AC的长度；
（2）求每级台阶的高度h．
（参考数据：sin12°≈0.2079，cos12°≈0.9781，tan12°≈0.2126．结果都精确到0.1cm）
身高1.65米的兵兵在建筑物前放风筝，风筝不小心挂在了树上．在如图所示的平面图形中，矩形CDEF代表建筑物，兵兵位于建筑物前点B处，风筝挂在建筑物上方的树枝点G处（点G在FE的延长线上）．经测量，兵兵与建筑物的距离BC=5米，建筑物底部宽FC=7米，风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上，点A距地面的高度AB=1.4米，风筝线与水平线夹角为37°．
（1）求风筝距地面的高度GF；
（2）在建筑物后面有长5米的梯子MN，梯脚M在距墙3米处固定摆放，通过计算说明：若兵兵充分利用梯子和一根米长的竹竿能否触到挂在树上的风筝？
（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）
如图，我国的一艘海监船在钓鱼岛A附近沿正东方向航行，船在B点时测得钓鱼岛A在船的北偏东60°方向，船以50海里/时的速度继续航行2小时后到达C点，此时钓鱼岛A在船的北偏东30°方向．请问船继续航行多少海里与钓鱼岛A的距离最近？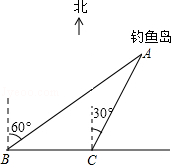
如图，小明在教学楼上的窗口A看地面上的B、C两个花坛，测得俯角∠EAB=30°，俯角∠EAC=45°．已知教学楼基点D与点C、B在同一条直线上，且B、C两花坛之间的距离为6m．求窗口A到地面的高度AD．（结果保留根号）
为缓解“停车难”问题，某单位拟建造地下停车库，建筑设计师提供了该地下停车库的设计示意图。按规定，地下停车库坡道口上方要张贴限高标志，以便告知停车人车辆能否安全驶入。(其中AB=9m，BC=0.5m)为标明限高，请你根据该图计算CE。(精确到0.1m)（参考数值
，
，
）
；
，其中
．
；
，再选择一个恰当的x值代入求值．
，其中x=2sin45°+1．
；（2）sin30°+cos30°•tan60°．
，其中
．
。 
。
粤公网安备 44130202000953号