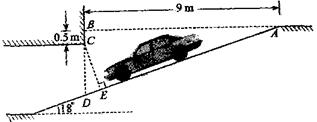
为缓解“停车难”问题，某单位拟建造地下停车库，建筑设计师提供了该地下停车库的设计示意图。按规定，地下停车库坡道口上方要张贴限高标志，以便告知停车人车辆能否安全驶入。(其中AB=9m，BC=0.5m)为标明限高，请你根据该图计算CE。(精确到0.1m)（参考数值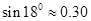
，
，
）
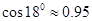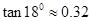相关试题
．
，并把它的解集在数轴上表示出来．
．
x+2≤1
x≤3．相关知识点
推荐套卷
为缓解“停车难”问题，某单位拟建造地下停车库，建筑设计师提供了该地下停车库的设计示意图。按规定，地下停车库坡道口上方要张贴限高标志，以便告知停车人车辆能否安全驶入。(其中AB=9m，BC=0.5m)为标明限高，请你根据该图计算CE。(精确到0.1m)（参考数值，，）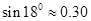
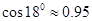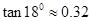粤公网安备 44130202000953号