如图,岸边的点A处距水面的高度AB为2.17米,桥墩顶部点C距水面的高度CD为23.17米.从点A处测得桥墩顶部点C的仰角为26°,求岸边的点A与桥墩顶部点C之间的距离.(结果精确到0.1米)(参考数据:sin26°=0.44,cos26°=0.90,tan26°=0.49)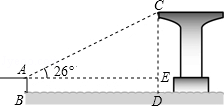
相关知识点
推荐套卷
如图,岸边的点A处距水面的高度AB为2.17米,桥墩顶部点C距水面的高度CD为23.17米.从点A处测得桥墩顶部点C的仰角为26°,求岸边的点A与桥墩顶部点C之间的距离.(结果精确到0.1米)(参考数据:sin26°=0.44,cos26°=0.90,tan26°=0.49)