如图是一种儿童的游乐设施﹣儿童荡板.小明想验证这个荡板上方的四边形是否是平行四边形,现在手头只有一根足够长的绳子,请你帮助他设计一个验证方案,并说明理由.
超速行驶是引发交通事故的主要原因之一,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在A处,距离大路(BC)为30米,一辆小轿车由西向东匀速行驶,测得此车从B处到C处所用的时间为5秒,∠BAC=60°.
(1)求B、C两点间的距离.
(2)请判断此车是否超过了BC路段限速40千米/小时的速度.(参考数据: ≈1.732,
≈1.732, ≈1.414)
≈1.414)
身高相等的四名同学甲、乙、丙、丁参加风筝比赛,四人放出风筝的线长、线与地面的夹角如下表(假设风筝线是拉直的),则四名同学所放的风筝中最高的是( )
| 同学 |
甲 |
乙 |
丙 |
丁 |
| 放出风筝线长 |
140m |
100m |
95m |
90m |
| 线与地面夹角 |
30° |
45° |
45° |
60° |
A.甲 B.乙 C.丙 D.丁
∠A是锐角,且sinA=cosA,则∠A的度数是( )
| A.30° | B.45° | C.60° | D.75° |
如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到1米,参考数据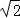 ≈1.4,
≈1.4,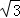 ≈1.7)
≈1.7)
如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进40海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海里C到航线AB的距离CD是( )
| A.20海里 | B.40海里 | C. 海里 海里 |
D. 海里 海里 |
如图,一艘海轮位于灯塔P的北偏东53°方向,距离灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处.
(1)在图中画出点B,并求出B处与灯塔P的距离(结果取整数);
(2)用方向和距离描述灯塔P相对于B处的位置.
(参考数据:sin53°=0.80,cos53°=0.60,tan53°=0.33, =1.41)
=1.41)
如图,利用标杆BE测量建筑物的高度,标杆BE高1.5m,测得AB=2m,BC=14cm,则楼高CD为 m.
如图,在矩形ABCD中,AB=6cm,点E、F分别是边BC、AD上一点,将矩形ABCD沿EF折叠,使点C、D分别落在点C′、D′处.若C′E⊥AD,则EF的长为 cm.
如图,若△ABC和△DEF的面积分别为S1、S2,则( )
A.S1=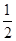 S2 S2 |
B.S1=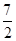 S2 S2 |
C.S1=S2 | D.S1=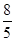 S2 S2 |
请阅读下列材料:
问题:如图(1),圆柱的底面半径为4cm,圆柱高AB为2cm,BC是底面直径,求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线,小明设计了两条路线:
路线1:高线AB+底面直径BC,如图(1)所示.
路线2:侧面展开图中的线段AC,如图(2)所示.
设路线1的长度为l1,则l1=AB+BC=2+8=10;
设路线2的长度为l2,则l2= =
= =
= ;
;
∵ =102﹣(4+16π2)=96﹣16π2=16(6﹣π2)<0
=102﹣(4+16π2)=96﹣16π2=16(6﹣π2)<0
∴ 即l1<l2
即l1<l2
所以选择路线1较短.
(1)小明对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为2cm,高AB为4cm”继续按前面的路线进行计算.(结果保留π)
①此时,路线1:l1= .路线2:l2= .
②所以选择哪条路线较短?试说明理由.
(2)请你帮小明继续研究:当圆柱的底面半径为2cm,高为hcm时,应如何选择上面的两条路线才能使蚂蚁从点A出发沿圆柱表面爬行到点C的路线最短.