河北省保定市博野县中考一模数学试卷
在一个不透明的口袋中,装有5个红球3个白球,它们除颜色外都相同,从中任意摸出一个球,摸到红球的概率为( )
A. |
B. |
C. |
D. |
下列计算,正确的是( )
| A.a6÷a2=a3 | B.(2x2)3=8x6 | C.3a2×2a2=6a2 | D.(-1)0×a=-a |
如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=32°,那么∠2的度数是( )
| A.32° | B.68° | C.58° | D.60° |
一元二次方程x2-4x+5=0的根的情况是( )
| A.有两个不相等的实数根 |
| B.有两个相等的实数根 |
| C.只有一个实数根 |
| D.没有实数根 |
观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…按此规律第5个图中共有点的个数是( )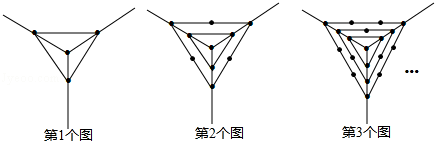
| A.31 | B.46 | C.51 | D.66 |
如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针方向转动一个角度到A1BC1的位置,使得点A,B,C1在同一条直线上,那么这个角度等于( )
| A.120° | B.90° | C.60° | D.30° |
如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点P(3,0),则a-b+c的值为( )
| A.0 | B.-1 | C.1 | D.2 |
如图,在梯形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是( )
| A.2 | B. |
C. |
D.2.5 |
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为 cm,则弦CD的长为( )
cm,则弦CD的长为( )
A. cm cm |
B.3cm | C.2 cm cm |
D.9cm |
如图所示,在边长为4的正方形ABCD中,以AB为直径的半圆与对角线AC交于点E,则图中阴影部分的面积为( )
| A.10-π | B.8-π | C.12-π | D.6-π |
如图所示,OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y= 在第一象限的图象经过点B,若OA2-AB2=18,则k的值为( )
在第一象限的图象经过点B,若OA2-AB2=18,则k的值为( )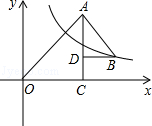
| A.12 | B.9 | C.8 | D.6 |
如图,在△ABC中,已知∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
①四边形CEDF有可能成为正方形;
②△DFE是等腰直角三角形;
③四边形CEDF的面积是定值;
④点C到线段EF的最大距离为 .
.
其中正确的结论是( )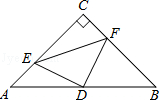
A.①④ B.②③ C.①②④ D.①②③④
已知,直线y=x绕原点O顺时针旋转90°得到直线l,直线l与反比例函数y= 的图象的一个交点为A(3,m),则k= .
的图象的一个交点为A(3,m),则k= .
如图,在Rt△ABC中,∠C=90°,∠B=37°,BC=32,则AC= .
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)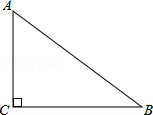
如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1,此时AP1=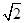 ;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=1+
;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=1+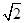 ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=2+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=2+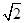 ;…,按此规律继续旋转,直至得到点P2014为止.则AP2014= .
;…,按此规律继续旋转,直至得到点P2014为止.则AP2014= .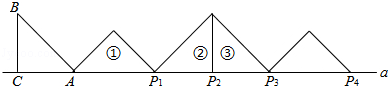
观察下列关于自然数的等式:
32-4×12=5 ①
52-4×22=9 ②
72-4×32=13 ③
…
根据上述规律解决下列问题:
(1)完成第四个等式:92-4× 2= ;
(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.
为了降低能源消耗,减少环境污染,国务院办公厅下发了“关于限制生产销售使用塑料购物袋的通知”(简称“限塑令”),并从2008年6月1日起正式实施.小宇同学为了了解“限塑令”后使用购物袋的情况,6月8日到某集贸市场对部分购物者进行了调查,据了解该市场按塑料购物袋的承重能力提供了0.1元,0.2元,0.3元三种质量不同的塑料袋.下面两幅图是这次调查得到的不完整的统计图(若每人每次只使用一个购物袋),请你根据图中的信息,回答下列问题:
(1)这次调查的购物者总人数是 ;
(2)请补全条形统计图,并说明扇形统计图中0.2元部分所对应的圆心角是 度,0.3元部分所对应的圆心角是 度;
(3)若6月8日到该市场购物的人数有3000人次,则该市场需销售塑料购物袋多少个?并根据调查情况,谈谈你的看法.
如图,在锐角三角形纸片ABC中,AC>BC,点D,E,F分别在边AB,BC,CA上.
(1)已知:DE∥AC,DF∥BC.
①判断
四边形DECF一定是什么形状?
②裁剪
当AC=24cm,BC=20cm,∠ACB=45°时,请你探索:如何剪四边形DECF,能使它的面积最大,并证明你的结论;
(2)折叠
请你只用两次折叠,确定四边形的顶点D,E,C,F,使它恰好为菱形,并说明你的折法和理由.
已知二次函数y=x2+bx+c图象的顶点坐标为(1,-4),与y轴交点为A.
(1)求该二次函数的关系式及点A坐标;
(2)将该二次函数的图象沿x轴翻折后对应的函数关系式是 .;
(3)若坐标分别为(m,n)、(n,m)的两个不重合的点均在该二次函数图象上,求m+n的值.
(4)若该二次函数与x轴负半轴交于点B,C为函数图象上的一点,D为x轴上一点,当以A、B、C、D为顶点的四边形是平行四边形时,请直接写出该平行四边形的面积
某商店经营儿童益智玩具,已知成批购进时的单价是20元.调查发现:销售单价是30元时,月销售量是230件,而销售单价每上涨1元,月销售量就减少10件,但每件玩具售价不能高于40元.设每件玩具的销售单价上涨了x元时(x为正整数),月销售利润为y元.
(1)求y与x的函数关系式并直接写出自变量x的取值范围.
(2)每件玩具的售价定为多少元时,月销售利润恰为2520元?
(3)每件玩具的售价定为多少元时可使月销售利润最大?最大的月利润是多少?
 的相反数是( )
的相反数是( )

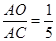 ,则
,则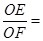 .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号