根据相似多边形的定义,我们把四个角分别相等,四条边成比例的两个凸四边形叫做相似四边形.相似四边形对应边的比叫做相似比.
(1)某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写"真"或"假" .
①四条边成比例的两个凸四边形相似; 命题)
②三个角分别相等的两个凸四边形相似; 命题)
③两个大小不同的正方形相似. 命题)
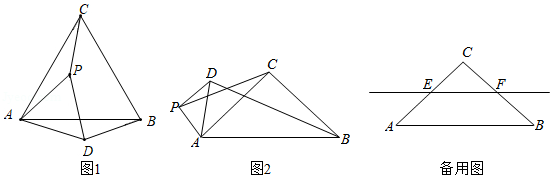
(2)如图1,在四边形 和四边形 中, , , .求证:四边形 与四边形 相似.
(3)如图2,四边形 中, , 与 相交于点 ,过点 作 分别交 , 于点 , .记四边形 的面积为 ,四边形 的面积为 ,若四边形 与四边形 相似,求 的值.
在中,已知
是
边的中点,
是
的重心,过
点的直线分别交
、
于点
、
.
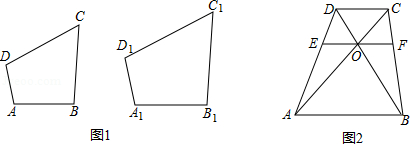
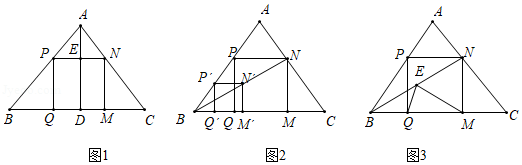
(1)如图1,当时,求证:
;
(2)如图2,当和
不平行,且点
、
分别在线段
、
上时,(1)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.
(3)如图3,当点在
的延长线上或点
在
的延长线上时,(1)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由.
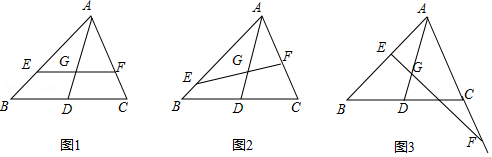
如图1,在中,
,
,点
为
边上的动点(点
不与点
,
重合).以
为顶点作
,射线
交
边于点
,过点
作
交射线
于点
,连接
.
(1)求证:;
(2)当时(如图
,求
的长;
(3)点在
边上运动的过程中,是否存在某个位置,使得
?若存在,求出此时
的长;若不存在,请说明理由.
小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.
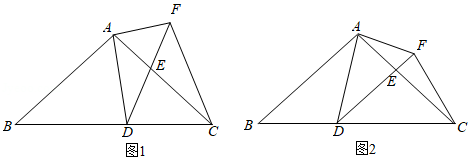
(1)温故:如图1,在中,
于点
,正方形
的边
在
上,顶点
,
分别在
,
上,若
,
,求正方形
的边长.
(2)操作:能画出这类正方形吗?小波按数学家波利亚在《怎样解题》中的方法进行操作:如图2,任意画,在
上任取一点
,画正方形
,使
,
在
边上,
在
内,连结
并延长交
于点
,画
于点
,
交
于点
,
于点
,得到四边形
.小波把线段
称为“波利亚线”.
(3)推理:证明图2中的四边形是正方形.
(4)拓展:在(2)的条件下,在射线上截取
,连结
,
(如图
.当
时,猜想
的度数,并尝试证明.
请帮助小波解决“温故”、“推理”、“拓展”中的问题.
请阅读下列材料,并完成相应的任务:
在数学中,利用图形在变化过程中的不变性质,常常可以找到解决问题的办法.著名美籍匈牙利数学家波利亚在他所著的《数学的发现》一书中有这样一个例子:请问如何在一个三角形 第一步,在 则有 下面是该结论的部分证明: 证明: 又
同理可得
|
任务:(1)请根据上面的操作步骤及部分证明过程,判断四边形的形状,并加以证明;
(2)请再仔细阅读上面的操作步骤,在(1)的基础上完成的证明过程;
(3)上述解决问题的过程中,通过作平行线把四边形放大得到四边形
,从而确定了点
,
的位置,这里运用了下面一种图形的变化是 .
.平移
.旋转
.轴对称
.位似
在中,
,
.点
是平面内不与点
,
重合的任意一点.连接
,将线段
绕点
逆时针旋转
得到线段
,连接
,
,
.
(1)观察猜想
如图1,当时,
的值是 ,直线
与直线
相交所成的较小角的度数是 .
(2)类比探究
如图2,当时,请写出
的值及直线
与直线
相交所成的较小角的度数,并就图2的情形说明理由.
(3)解决问题
当时,若点
,
分别是
,
的中点,点
在直线
上,请直接写出点
,
,
在同一直线上时
的值.