小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.
(1)温故:如图1,在中,于点,正方形的边在上,顶点,分别在,上,若,,求正方形的边长.
(2)操作:能画出这类正方形吗?小波按数学家波利亚在《怎样解题》中的方法进行操作:如图2,任意画,在上任取一点,画正方形,使,在边上,在内,连结并延长交于点,画于点,交于点,于点,得到四边形.小波把线段称为“波利亚线”.
(3)推理:证明图2中的四边形是正方形.
(4)拓展:在(2)的条件下,在射线上截取,连结,(如图.当时,猜想的度数,并尝试证明.
请帮助小波解决“温故”、“推理”、“拓展”中的问题.

相关知识点
推荐套卷
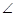 ACB=90°,
ACB=90°,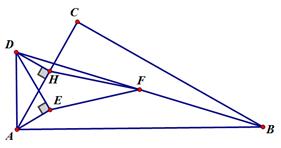
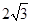 ,求AB,BD的长。
,求AB,BD的长。 B=
B=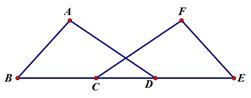
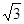 ≈1.73)
≈1.73)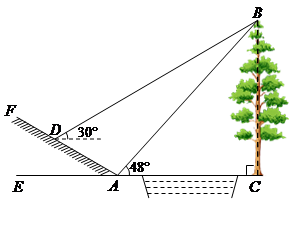

 粤公网安备 44130202000953号
粤公网安备 44130202000953号