初中数学相似多边形的性质试题

把一个矩形剪去一个正方形，若剩下的矩形与原矩形相似，则原矩形的长边与短边之比为      ．

两个相似三角形的面积比为4：9，那么它们对应中线的比为        ．

如果线段c是a、b的比例中项，且a=4，b=9，则c=        ．

如图，在△ABC中，EF∥BC，，S_{四边形BCFE}=8，则S_△ABC等于（     ）

A．9

B．10

C．12

D．13

如图所示，在△ABC中，BA=BC=20cm，AC=30cm，点P从点A出发，沿AB以4cm/s的速度向点B运动，同时点Q从C点出发，沿CA以3cm/s的速度向点A运动，设运动时间为x秒．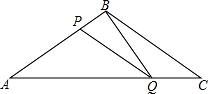

（1）当x为何值时，BP=CQ；
（2）以A、P、Q为顶点的三角形能否与以C、Q、B为顶点的三角形相似？若能，求出x的值；若不能，请说明理由．

如图，已知AB为⊙O的直径，PA与⊙O相切于点A，线段OP与弦AC垂直并相交于点D，OP与⊙O相交于点E，连接BC．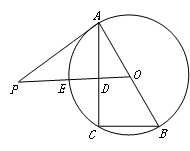

（1）求证：△PAD∽△ABC；
（2）若PA=10，AD=6，求AB的长．

如图，已知∠1=∠2，AB•AC=AD•AE．求证：∠C=∠E．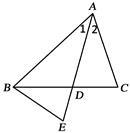

如图，在△ABC中，D、E分别是AB、AC的中点，则△ADE与△ABC的面积比为              ．

两个相似三角形的对应边分别是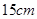和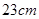，它们的周长相差，则这两个三角形的周长分别是（   ）

A．，	B．，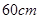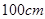
C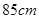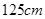．，	D．，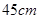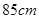

如图△ABC与△DEA是两个全等的等腰直角三角形，∠BAC=∠D=90°，△DEA 绕点A旋转，边AD、AE与BC分别与AD、AE相交于点F、G，CB=5．
回答下列问题：

（1）求证：△GAF∽△GBA；
（2）求证：AF²=FG•FC；
（3）设y=AF²+AG²，FG=x，求y与x的函数关系式；（不要求写出自变量的取值范围）
（4）探究BF²、FG²、GC²之间的关系，证明你的结论．

如图，已知点I是△ABC的内心，AI交BC于D，交外接圆O于E，求证：

（1）IE=EC；
（2）IE²=ED•EA．

在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B．

（1）求证：△ADF∽△DEC；
（2）若AB=4，AD=3，AE=3，求AF的长．

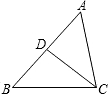
如图所示，给出下列条件：①∠B=∠ACD；②∠ADC=∠ACB；③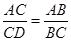；④AC²=AD•AB，其中单独能够判定△ABC∽△ACD的有            ．

如图已知四边形ABCD是⊙O的内接四边形，且AB=CD=5，AC=7，BE=3，下列命题：
①△AED∽△BEC
②∠AEB=90°
③∠BDA=45° 
④图中全等的三角形共有3对．
其中正确的命题有（    ）个．

A．1

B．2

C．3

D．4

如图1，OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=5，OC=4．在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处，边AE上有一动点P（不与A，E重合）自A点沿AE方向向E点匀速运动，运动的速度为每秒1个单位长度，设运动的时间为t秒（0＜t＜5），过P点作ED的平行线交AD于点M，过点M作AE的平行线交DE于点N．

（1）直接写出 D，E 两点的坐标，D（         ），E（           ）
（2）求四边形PMNE的面积S与时间t之间的函数关系式；当t取何值时，S有最大值？
（3）当t为何值时，DP平分∠EDA？
（4）当t为何值时，以A，M，E为顶点的三角形为等腰三角形，并求出相应的时刻点M的坐标．