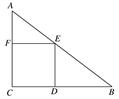
如图,已知点A是第一象限内横坐标为 的一个定点,AC⊥x轴于点M,交直线y=-x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是 .
的一个定点,AC⊥x轴于点M,交直线y=-x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是 .
如图,直角三角形ABC中,∠ACB=900,AB=10, BC=6,在线段AB上取一点D,作DF⊥AB交AC于点F.现将△ADF沿DF折叠,使点A落在线段DB上,对应点记为A1;AD的中点E的对应点记为E1.若△E1FA1∽△E1BF,则AD= .
如图,CD是⊙O的直径,弦AB⊥CD,垂足为点M,AB=20,分别以DM、CM为直径作两个大小不同和⊙O1和⊙O2,则图中所示阴影部分的面积为 .(结果保留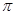 )
)
正方形ABCD边长为a,点E、F分别是对角线BD上的两点,过点E、F分别作AD、AB的平行线,如图所示,则图中阴影部分的面积之和等于 .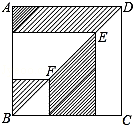
如图,小红作出了边长为1的第1个正三角形△A1B1C1,算出了正△A1B1C1的面积,然后分别取△A1B1C1三边的中点A2B2C2,作出了第二个正三角形△A2B2C2,算出第2个正△A2B2C2的面积,用同样的方法作出了第3个正△A3B3C3,算出第3个正△A3B3C3的面积,依此方法作下去,由此可得第n次作出的正△AnBnCn的面积是 .
如图7,在△ABC中,AB=AC=5,BC=6,点E、F分别在AB、BC边上,将△BEF沿直线EF翻折后,点B落在对边AC的点为B',若△B'FC与△ABC相似,那么BF= .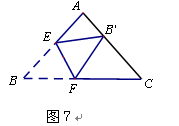
如图,点A1、B1、C1分别是△ABC的三边BC、AC、AB的中点,点A2、B2、C2分别是△A1B1C1的边B1C1、A1C1、A1B1的中点,依此 类推,则△AnBnCn与△ABC的面积比为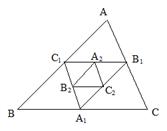
如图,已知Rt△ABC,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连结BE1交CD1于D2;过D2作D2E2⊥AC于E2,连结BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点E4、E5、…、En,分别记△BCE1、△BCE2、△BCE3···△BCEn的面积为S1、S2、S3、…Sn. 则Sn= ▲ S△ABC(用含n的代数式表示).
如图,点P是矩形ABCD的边AD的一个动点,矩形的两条边AB、BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是__
如图,在Rt△ABC中,斜边AB的长为35,正方形CDEF内接于△ABC,且其边长为12,则△ABC的周长为 .